Primitive
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Linaben
- Messages: 8
- Enregistré le: 31 Aoû 2019, 13:28
-
 par Linaben » 31 Aoû 2019, 13:48
par Linaben » 31 Aoû 2019, 13:48
Bonjour, je dois résoudre un exercice avant ma rentrée (lundi) et cela fait 1 semaine que je suis bloquée sur 2 équations (j'ai les résultats donnés dans l'énoncé mais je n'arrive pas à trouver la méthode de résolution)
Soit :
Primitive de. (x^2 / racinex).dx
Primitive de e^(ax).cos(bx).dx
Si quelqu'un peut m'expliquer

Merci par avance , bonne journée !!

-
Mimosa
- Membre Relatif
- Messages: 432
- Enregistré le: 19 Aoû 2016, 16:31
-
 par Mimosa » 31 Aoû 2019, 13:51
par Mimosa » 31 Aoû 2019, 13:51
Bonjour
Pour le premier remarque que
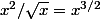
.
Pour le second fais deux fois des intégrations par parties en dérivant la fonction trigonométrique.
-
Linaben
- Messages: 8
- Enregistré le: 31 Aoû 2019, 13:28
-
 par Linaben » 31 Aoû 2019, 14:24
par Linaben » 31 Aoû 2019, 14:24
Merci beaucoup, j'ai tellement chercher compliqué pour la première que je suis passé à coté de la solution toute simple.
Je vais réessayer le deuxième.
Encore merci bonne journée.
-
Mimosa
- Membre Relatif
- Messages: 432
- Enregistré le: 19 Aoû 2016, 16:31
-
 par Mimosa » 31 Aoû 2019, 14:42
par Mimosa » 31 Aoû 2019, 14:42
Bon courage.
-
Linaben
- Messages: 8
- Enregistré le: 31 Aoû 2019, 13:28
-
 par Linaben » 31 Aoû 2019, 14:45
par Linaben » 31 Aoû 2019, 14:45
Mimosa a écrit:Bonjour
Pour le premier remarque que
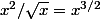
.
Pour le second fais deux fois des intégrations par parties en dérivant la fonction trigonométrique.
Rebonjour,
J'ai réaliser mes deux intégration par partie mais je n'arrive toujours pas à terminer mon équation il me reste toujours :
........ x (1/a).intégrale { (b^2).cosbx.(e^ax) }
Pouvez vous m'indiquer la méthode ?
-
Mimosa
- Membre Relatif
- Messages: 432
- Enregistré le: 19 Aoû 2016, 16:31
-
 par Mimosa » 31 Aoû 2019, 15:09
par Mimosa » 31 Aoû 2019, 15:09
Tu passes ça dans le premier membre!
Tu peux aussi chercher une primitive de la forme
+\beta \cos(bx)))
-
Linaben
- Messages: 8
- Enregistré le: 31 Aoû 2019, 13:28
-
 par Linaben » 31 Aoû 2019, 15:24
par Linaben » 31 Aoû 2019, 15:24
Je suis désolée je ne comprends pas

-
Linaben
- Messages: 8
- Enregistré le: 31 Aoû 2019, 13:28
-
 par Linaben » 31 Aoû 2019, 15:34
par Linaben » 31 Aoû 2019, 15:34
Voici ce que j'ai fais
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 31 Aoû 2019, 15:50
par Pisigma » 31 Aoû 2019, 15:50
Bonjour,
je laisserai répondre
Mimosa.
Quand tu auras finalisé ton calcul, voici une autre méthode utilisant les nombres complexes:
}=\Re(e^{ax}e^{ibx})=\Re(e^{(a+ib)x}))
-
Mimosa
- Membre Relatif
- Messages: 432
- Enregistré le: 19 Aoû 2016, 16:31
-
 par Mimosa » 01 Sep 2019, 15:05
par Mimosa » 01 Sep 2019, 15:05
Voici un exemple plus facile que le tien, mais avec la même méthode:
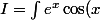\,dx=e^x\cos(x)+\int e^x\sin(x)\,dx=e^x\cos(x)+e^x\sin(x)-\int e^x\cos(x)\,dx=e^x\cos(x)+e^x\sin(x)-I)
d'où
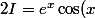+e^x\sin(x))
Toi tu auras probablement à discuter en fonction de

et

.
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 01 Sep 2019, 17:34
par fibonacci » 01 Sep 2019, 17:34
bonsoir,
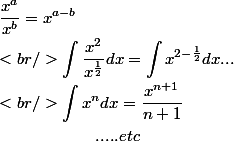
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités


.