Démonstration
5 messages
- Page 1 sur 1
démonstration
par abdelmalek.2008 » 28 Mai 2019, 17:39
Bonjour, Comment démontrer que: 
Modifié en dernier par abdelmalek.2008 le 28 Mai 2019, 17:50, modifié 1 fois.
Re: démonstration
par aviateur » 28 Mai 2019, 22:13
Bjr
a-b=0 mod 100 ssi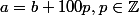
alors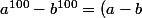\sum_{k=0}^{99} a^k b^{99-k})
mais chaque terme de la somme mod 100 vaut: . En effet
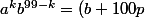^k b^{99-k}= b ^k b^{99-k} +0 =b^{99})
mod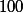 
bon c'est corrigé
D'où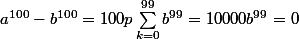
mod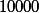 
a-b=0 mod 100 ssi
alors
mais chaque terme de la somme mod 100 vaut: . En effet
bon c'est corrigé
D'où
Modifié en dernier par aviateur le 29 Mai 2019, 08:21, modifié 1 fois.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :