Equation et factorisation racine

[Scrounch]

Bien le bonjour,

Je me surprend ce matin a bloquer sur une équation, puis je me rends compte que je ne suis pas au point pour factoriser des racines. Voici l'équation qui est utilisée dans le domaine du lancer de projectile :



Je souhaite isoler la variable v d'un côté de l'équation mais la racine me donne du fil a retorde.
Quelqu'un parmi vous est-il plus à l'aise ?

D'avance merci

[hdci]

Bonjour,

Si je comprends bien : v est l'inconnue, et d, a, g, h sont des indéterminées (des paramètres) ? Et tu souhaites connaître v en fonction de ces autres paramètres ?

Si c'est le cas, il faut effectivement "supprimer" la racine carrée puisqu'il y a du v dedans, et le mieux est d'élever au carré.
Mais si la racine est dans une somme, le double produit va continuer à faire apparaître une racine. Pour éviter cela, il faut d'abord isoler la racine

Cela donne



Là quand tu élèves au carré, plus de racine carrée mais de l'autre côté du a du et du

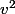
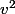
Ceci dit comme à gauche tu as aussi du , tu pose et tu as une équation du second degré en V. Il y a donc 0, 1 ou 2 solutions pour V, et comme V est un carré on ne conserve que les solutions positives de V ce qui donne pour chacune d'elle deux valeurs possibles pour v

(PS j'ai supposé qu'on travaille dans les réels puisque cela ressemble bigrement à une histoire de vitesse, d'accélération et d'angle de mouvement...)

[Scrounch]

Bonjour hdci,

Comme tu as deviné, et j'aurais dû le préciser, d, a, g et h sont bien les paramètres et v est l'inconnue.
En fait, d est une distance d'impact par rapport au lancer, a est l'angle de lancer par rapport à l'horizontale, g est l'accélération de la gravité, et h correspond à hauteur de lancer - hauteur atterrissage. Le tout en unités SI.

Ta proposition semble être le bon résonnement, je finis le calcul à partir de ta réponse et je redonne le résultat.

Merci pour ta réponse claire