Bonsoir svp pouvez vous me dire pourquoi la primitive de g*sin(alpha)=(g*sin(alpha))t au lieu de
(-g*cos(alpha))?
Maths primitive
11 messages
- Page 1 sur 1
Re: Maths primitive
J'imagine qu'il s'agit d'une conséquence du principe fondamental de la dynamique auquel cas  est constant. Pour faciliter les choses, dis toi que
est constant. Pour faciliter les choses, dis toi que ) est une constante, on la note
est une constante, on la note  , alors
, alors =C) donc par intégration,
donc par intégration, =Ct+A=g\sin(\alpha)t+A) où
où  est une constante (c.f ton cours de maths sur les primitives et/ou l'intégration). Les conditions initiales te permettent de calculer la valeur de la constante A et tu peux refaire le même raisonnement avec
est une constante (c.f ton cours de maths sur les primitives et/ou l'intégration). Les conditions initiales te permettent de calculer la valeur de la constante A et tu peux refaire le même raisonnement avec 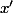 .
.
Re: Maths primitive
mgftbl a écrit:Mon énoncé complet est de résoudre l'équation x''=g*sin(alpha).
d'où l'intérêt de donner ton énoncé complet
Re: Maths primitive
Après il y a une autre question qui parle d'une pierre de masse 0,1 kg qui est lancée horizontalement à la vitesse de 1/√2 m/s depuis une hauteur de 1 mètre et de décrire sa trajectoire.
Re: Maths primitive
Salut,
Tout dépend de la signification du symbole primé. Si c'est une dérivée par rapport au temps, alors une primitive est bien t)
Si c'est plutôt qui est la variable alors c'est plutôt ta réponse qui fait du sens. Mais il est évident que dans un contexte de mécanique classique, le temps est la variable et donc ta réponse ne fait pas de sens.
qui est la variable alors c'est plutôt ta réponse qui fait du sens. Mais il est évident que dans un contexte de mécanique classique, le temps est la variable et donc ta réponse ne fait pas de sens.
Tout dépend de la signification du symbole primé. Si c'est une dérivée par rapport au temps, alors une primitive est bien
Si c'est plutôt
Re: Maths primitive
Considères les coordonnées x, y et z de la masse dans le référentiel terrestre supposé galiléen, on note  des vecteurs unitaires dirigés respectivement selon les axes
des vecteurs unitaires dirigés respectivement selon les axes ,\,(Oy)) et la verticale
et la verticale ) et avec la vitesse initiale de la balle
et avec la vitesse initiale de la balle 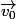 dirigée par exemple selon
dirigée par exemple selon ) de sorte que
de sorte que  . La masse n'est soumise qu'à son poids
. La masse n'est soumise qu'à son poids  donc d'après le principe fondamental de la dynamique :
donc d'après le principe fondamental de la dynamique :



11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
