équation differentielle ( probleme de cauchy)

[peed5]

Est une solution maximale.

Sur où sur , car il y a unicité de la solution.

[mathelot]

bonsoir,
on pose:

où K est une fonction dérivable sur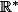

il vient:







on intégre












y est définie sur l'intervalle si C>0
y est définie sur si C<0

La condition initiale donne:





PS : la fonction signe de x, notée sgn(x) vaut 1 si x>0 , -1 si x<0 et 0 si x=0
en particulier, sgn(y) |y|=y

[aviateur]

€xxxxxxx

[peed5]

Ta note est 0/20 pour cet epsilon de la question 1) car tu ne démontres rien du tout.

La question 1) nous demande de préciser cet intervalle de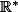 , toi tu donnes comme intervalle.

C’est juste que est une solution maximale. Mais l’exercice ne souhaite pas qu’on traite le cas .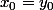

J’ai déjà dit cette après-midi que j’ai répondu à la question 1) hier à 00h21 et que je suis sûr de ma réponse.

Tu souhaites répéter ce que j'ai écrit hier à 00h21 autrement mes faux par rapport à l'exercice, ce qui énerve en plus c’est que tu dis que ça n’a pas de sens.

[peed5]

J’ai posé 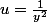et j’ai résolu l’équation différentielle, il me reste le début de la question 2), c’est-à-dire « Montrer que si , non identiquement nulle, est solution de alors ne s’annule pas.»

Si quelqu'un pouvait m'aider.
Merci d’avance.

[tournesol]

On a unicité de la solution maximale dans et dans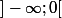
D'autre part la fonction nulle est solution sur R , donc sur chacun de ces deux intervalles .
Donc si une solution s'annule sur un de ces intervalle , elle est identiquement nulle .
D'où la contraposée .
Il est regrettable que tu te prennes la tête avec aviateur car il est très compétant , et disponible . Il aide de nombreux étudiants et quelquefois des profs dont je fais partie .

[tournesol]

@mathelot
Le signe d'une solution y est celui de , donc tu dois remplacer au numérateur par sa valeur absolue .

[mathelot]

@tournesol: j'ai corrigé