Probléme de Cauchy
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
othoo
- Membre Naturel
- Messages: 32
- Enregistré le: 23 Aoû 2006, 12:37
-
 par othoo » 28 Fév 2007, 19:57
par othoo » 28 Fév 2007, 19:57
bonjour, j'arrive pas à comprendre la résolution de l'équadiff Y'=-Y².Voici le corrigé que je n'arrive pas à comprendre :
L'application f : (t,y) --> y² est de classe C1 sur R², d'après le théorème de Cauchy, il existe une solution maximale unique de E g telle que g(t0)=y0
Soit I l'ensemble de définition de g, supposons que g s'annule : la solution nulle étant une solution de E, par unicité des solutions maximales aux problèmes de Cauchy g est alors nulle merci d'avance
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 28 Fév 2007, 20:20
par yos » 28 Fév 2007, 20:20
Bonjour.
Le raisonnement que tu cites dit seulement que l'équation n'a pas de solution qui s'annule en dehors de la fonction nulle. On peut donc supposer que ta solution ne s'annule pas.
La fonction inverse est solution sur tout intervalle ne contenant pas 0.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 28 Fév 2007, 20:23
par fahr451 » 28 Fév 2007, 20:23
bonsoir
que ne comprends tu pas dans cette preuve ?
-
othoo
- Membre Naturel
- Messages: 32
- Enregistré le: 23 Aoû 2006, 12:37
-
 par othoo » 28 Fév 2007, 20:30
par othoo » 28 Fév 2007, 20:30
je comprend pas pourquoi l'annulation de g en un point entraine l'annulation de la fonction g dans tout l'intervalle I
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 28 Fév 2007, 20:34
par fahr451 » 28 Fév 2007, 20:34
c'est justifié en toute lettre
d'accord pour l'unicité du problème de cauchy ?
-
mathelot
 par mathelot » 28 Fév 2007, 21:04
par mathelot » 28 Fév 2007, 21:04
Bonsoir,
On a l'inégalité suivante:
si dy/dt=f(x,y) est une équa diff, et f k-lipschitzienne
si
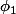
et

sont deux solutions de cette équation, de valeurs initiales
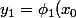 \mathrm{et} y_{2}=\phi_{2}(x_{0}))
:
-\phi_{2}(x)| \leq |y_{1}-y_{2}|e^{k|x-x_{0}|})
-
othoo
- Membre Naturel
- Messages: 32
- Enregistré le: 23 Aoû 2006, 12:37
-
 par othoo » 28 Fév 2007, 21:49
par othoo » 28 Fév 2007, 21:49
vraiment j'ai pas compris le raisonement :cry: .pour l'unicité de la solution c'est le théorème de Cauchy qui l'assure je ne vois pas où est le probléme
merci d'avance

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 28 Fév 2007, 22:55
par nuage » 28 Fév 2007, 22:55
Salut,
on reprend tout depuis le début :
Il y a une solution

et une seule telle que
=y_0)
ça c'est Gauchy.
La fonction

est solution (facile à vérifier).
Conclusion : si
=0)
pour un certain

alors la fonction

est la fonction

.
A part ça les solutions sont les fonctions

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
