équation differentielle ( probleme de cauchy)

[peed5]

Bonjour, je suis bloqué dans le début de cet exercice si vous pouvez m’aider.

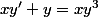
Soit le problème de Cauchy : avec la condition initiale .

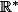
1)vérifier qu’il existe une solution maximale de sur un intervalle de à préciser.

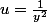
2)Montrer que si , non identiquement nulle, est solution de alors ne s’annule pas. Poser et résoudre l’équation différentielle.

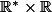
pour le 1) La fonction est de classe sur l’ouvert , d’après le théorème de Cauchy Lipschitz, le problème de Cauchy :



Admet une seule solution.

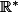
Comment puis-je préciser l’intervalle de des solutions ?

Tout ce dont je sais qu’il s’agit d’un intervalle ouvert contenant .

le début de la question 2) aussi je n’ai pas compris.

Je vous remercie d'avance.

[aviateur]

x

[peed5]

Bonsoir et merci pour la réponse.

D’après le théorème de Cauchy-Lipschitz, le problème de Cauchy admet une seule solution maximale.
Donc :
Si , cette solution maximale est :
Définie sur si
Définie sur si
Je pense que c’est tout ce qu’on peut dire non ? après on va étudier le cas

[peed5]

1- Sur l’autre forum, je n’ai pas confiance de ce qui raconte ces deux personnes
2- Je n’ai pas compris ce qui me raconte
3- Les informations je les ai trouvées tout seul.
4- Je sais très bien repérer si l’aide que je reçois est logique et correcte ou pas.
5- Jusqu’au présent je n’ai pas reçu d’aide, ni ici, ni dans l’autre forum.
6- Je vais encore m’inscrire sur d’autres forums, jusqu’à ce que je comprenne, surtout la deuxième question.

[peed5]

La réponse à la question 1) je l’ai écrit à 00:21 ( et je suis sûr de ce que j’écris ). Et ceci montre que je connais ce que ça veut dire une solution maximale.
Je pense que tu es un des deux débiles qui se trouve dans l’autre forum, sinon tu vas être un nouveau de ce forum.
Non, je ne vais pas à bibmath , il y a que des débiles comme ici.

Ps : Je n’ai pas eu d’indication de réponse.

[aviateur]

x

[peed5]

On ne peut pas répondre à la question si l’on ne résout pas l’équation.
Tout ce qu’on peut dire c’est ce que j’ai écrit à 00 :21
À part ça, donne-moi cet intervalle, toi qui prétends comprendre la solution maximale du théorème de Cauchy.
Si tu penses que c’est faux ce que j’ai écrit à 00:21, ça ne sert à rien que je continue à parler avec toi.

[aviateur]

x

[peed5]

Je suis désolé, mais c’est toi qui as baissé le niveau dans ton deuxième message.
Un conseil : n’aide plus personne, car :
1- Tu ne sais rien du tout et vas apprendre les maths avant de venir ici.
2- On va supposer que tu sais un peu en math, franchement va faire autre chose que venir aider dans des forums, car d’après avoir lu quelques messages que tu postes ici, crois-moi que tu n’aides pas les gens, mais tu compliques encore le problème.
Alors j’espère qu’au moins tu appris quelque chose qui est : « si tu ne respectes pas les gens, les gens ne vont pas te respecter »
J’imagine bien que tu as beaucoup de soucis dans ta vie.

[peed5]

Tu as baissé le niveau dans ton deuxième message effacé en plus. OK, on peut comprendre que tu as effacé ton premier message, que tu crois qu’il s’agit d’une aide (c’est effacé dans ma tête avant que tu l’effaces).

[aviateur]

x

[Lostounet]

Allons messieurs,
Dommage d'en arriver là.

Souhaitez-vous poursuivre la discussion de manière respectueuse et productive ou bien devrais-je la fermer?

[peed5]

Bonsoir,

Monsieur il me provoque avec des messages et puis il supprime.

Je suis venu ici pour l’aide, il n’est pas capable de m’aider et il n’a pas le niveau pour ça, de plus il a vu que j’ai déjà été dans un autre forum là où je n’ai rien compris, alors il me suit ici pour me perturber encore.

Donc il est au courant, que soit, disons je n’ai pas compris dans d’autres forums, alors il nous montre de quoi il est capable et il nous explique l’exercice en détaille, comme ça on va juger son niveau, s’il peut aider les gens ou pas.

Sinon il laisse mon sujet tranquille et il n’intervient pas en attendant un autre qui peut m’expliquer.

[aviateur]

Bonsoir

[aviateur]

Bonsoir
@lostounet je suis désolé toute cette interprétation est fausse.
Le fait d'avoir retiré un message n'a rien avoir avec ce qu'il dit et
c'est tout de même fort, sur ce pb j'étais venu pour l'aider.
Je suis complètement écoeuré de tout ça,xxxxc

[peed5]

Mon avis personnel c’est que tu n’aides pas les gens, mais au pire tu compliques leurs problèmes.
La preuve : dans le cas de mon exercice et comme tu as vu que j’ai déjà été dans d’autres forums et ça n’allait pas, si tu as envie d’aider c’est d’expliquer en détail la première question, chose que ta pas fait et tu n’es pas capable de le faire.

[aviateur]

Xxxxxxxx

[peed5]

En math parfois on a besoin même de comprendre la solution de l’exercice. Et c’est le cas ici, je cherche une solution pour la comprendre, dans l’autre forum je suis sûr à 100% que c’est faux. Et si tu crois que c’est juste, cela veut dire que toi-même tu n’as pas compris et tu as besoin de qu’un qui t’explique.

[aviateur]

Arrête un peu et réponds à ma question.

[peed5]

On dit que (y,I) est une solution maximale d’une l'équation différentielle si elle n'admet pas de prolongement. Autrement dit, pour toute autre solution.
Si et pour tout alors