Bonjour,
J'ai du mal avec le chapitre d'analyse surtout par rapport aux contraintes linéaires
L'énoncé est : "Déterminer les extrema de la fonction f(x,y,z,t) = x²+2y²+3z²+4t² sous les contraintes x+y=2 et z+t=0"
On a pas vu de méthodes pour l'instant, alors est-ce qu'il faut utiliser le théorème suivant : " Si f est de classe C1 sur R^4 et présente un extremum local en a sous la contrainte C non critique, alors il existe un réel k tel que : f(a)=2 et le gradient de f(a) = k(gradient(g)(a)) " où g est la fonction définie au dessus g(x,y) = x+y
Et répéter cette méthode pour la 2e fonction, en résolvant le système linéaire associé pour trouver l'extremum?
Parce que là, la fonction de base est dans R^4 et les contraintes dans R^2 donc je vois pas comment résoudre le système
J'espère avoir été clair
Extremum sous contrainte
11 messages
- Page 1 sur 1
Re: Extremum sous contrainte
C'est plus facile que celà . Il te suffit de remplacer t par -z et y par 2-x .
on obtient après calculs
l'annulation du gradient donne x=4/3 et z=0 . Donc le seul extremum possible est obtenu pour ces deux valeurs . Or la factorisation de l'expression précédente donne^2+7z^2+\frac{8}{3})
Le minimum absolu de cette expression est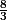 , atteint pour les valeurs précedentes .
, atteint pour les valeurs précedentes .
C'est donc le seul extremum de f et il est atteint pour x=4/3 , y=2-x=2/3 , z=0 , et t=-z=0 .
on obtient après calculs
l'annulation du gradient donne x=4/3 et z=0 . Donc le seul extremum possible est obtenu pour ces deux valeurs . Or la factorisation de l'expression précédente donne
Le minimum absolu de cette expression est
C'est donc le seul extremum de f et il est atteint pour x=4/3 , y=2-x=2/3 , z=0 , et t=-z=0 .
Re: Extremum sous contrainte
Merci pour ta réponse, alors j'avais tenté cette méthode aussi, sauf que pour l'expression de f en fonction des nouvelles variables, je trouve 3x² + 7z² -8x + 8, et je vois vraiment pas comment tu obtiens le 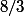 ..
.. 
Re: Extremum sous contrainte
Lol , tu trouves la même expression que moi . As tu vu sa réduction à 3 termes qui est dans mon message ?
Re: Extremum sous contrainte
Lol de moi . Il n'y a pas de  3 dans l'expression développée , mais il y est dans la réduction que tu n'as qu'a developper et réduire pour t'en convaincre (en retrouvant ton expression) .
3 dans l'expression développée , mais il y est dans la réduction que tu n'as qu'a developper et réduire pour t'en convaincre (en retrouvant ton expression) .
 3 dans l'expression développée , mais il y est dans la réduction que tu n'as qu'a developper et réduire pour t'en convaincre (en retrouvant ton expression) .
3 dans l'expression développée , mais il y est dans la réduction que tu n'as qu'a developper et réduire pour t'en convaincre (en retrouvant ton expression) .Re: Extremum sous contrainte
Salut,
x²+2y²+3z²+4t²
= x² + 2(2-x)²+3z²+4z²
= x² + 2(4+x²-4x)+3z²+4z²
= 3x² - 8x + 7z² + 8
= (V3.x - 4/V3)² - (4/V3)² + 7z² + 8
= (V3.x - 4/V3)² + 7z² + 8 /3
Dont le min est 8 /3 pour x = 4/3, z = 0, t = 0 et y = 2 - 4/3 = 2/3

x²+2y²+3z²+4t²
= x² + 2(2-x)²+3z²+4z²
= x² + 2(4+x²-4x)+3z²+4z²
= 3x² - 8x + 7z² + 8
= (V3.x - 4/V3)² - (4/V3)² + 7z² + 8
= (V3.x - 4/V3)² + 7z² + 8 /3
Dont le min est 8 /3 pour x = 4/3, z = 0, t = 0 et y = 2 - 4/3 = 2/3
Re: Extremum sous contrainte
La question est : determiner les extrémas et pas seulement le minimum absolu .
Re: Extremum sous contrainte
Salut
Evidemment la simplicité de l'exercice (dû à la contrainte) fait qu'on a intérêt à se débarrasser de la contrainte
et de se ramener à une recherche d'extremum d'une fonction à 2 variables.
Mais si on relit la question, il semblerait que le but de l'exercice serait d'appliquer le théorème évoqué (mais non formulé) par JohnnySuave.
C'est à dire que si l'équation de la contrainte est=b) alors on est amené à chercher les extremums locaux
alors on est amené à chercher les extremums locaux
 qui vérifient
qui vérifient  \in \nabla g(a).)
Evidemment la simplicité de l'exercice (dû à la contrainte) fait qu'on a intérêt à se débarrasser de la contrainte
et de se ramener à une recherche d'extremum d'une fonction à 2 variables.
Mais si on relit la question, il semblerait que le but de l'exercice serait d'appliquer le théorème évoqué (mais non formulé) par JohnnySuave.
C'est à dire que si l'équation de la contrainte est
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
