bonjour,
resoudre cos2x=1/4
cos(x)=1/2 ou cos(x)= -1/2
pour cos(x)=1/2 on ecrit:
cos(x)=cos(/3) ou cos(x)=cos(-/3)
x=/3+2kr ou x=-/3+2k
et pour cosx=(-1/2) on ecrit :
cos(x)=cos(-1/2)
cos(x)=cos(-/3)
cos(x)=(2/3)
donc je fais cela ?
x=2/3+2k ou x=-2/3+2k
svp faites moi signe si vous allez repondre
Calcul trigonometrique
3 messages
- Page 1 sur 1
Re: calcul trigonometrique
Bonjour;
=\dfrac{1}{4}=\left(\dfrac{1}{2}\right)^2) ; donc :
; donc : -\left(\dfrac{1}{2}\right)^2=0) ;
;
donc :-\dfrac{1}{2})(cos(x)+\dfrac{1}{2})=0) ; donc :
; donc : -\dfrac{1}{2}=0) ou
ou +\dfrac{1}{2}=0) .
.
Pour :-\dfrac{1}{2}=0) on a :
on a : =\dfrac{1}{2}=cos(\dfrac{\pi}{3})) ; donc :
; donc : 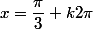 ou
ou 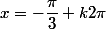 avec
avec  ;
;
Pour :+\dfrac{1}{2}=0) on a :
on a : =-\dfrac{1}{2}=-cos(\dfrac{\pi}{3})=cos(\pi-\dfrac{\pi}{3})=cos(\dfrac{2\pi}{3})) ;
;
donc :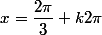 ou
ou 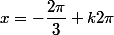 avec
avec  .
.
Maintenant je te laisse tracer le cercle trigonométrique pour y faire figurer ces solutions : une petite remarque
te permettra de simplifier l'ensemble des solutions .
donc :
Pour :
Pour :
donc :
Maintenant je te laisse tracer le cercle trigonométrique pour y faire figurer ces solutions : une petite remarque
te permettra de simplifier l'ensemble des solutions .
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
