Petit problème de dérivée
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Nostra8
- Messages: 6
- Enregistré le: 22 Fév 2019, 16:45
-
par Nostra8 » 22 Fév 2019, 17:08
Bonjour à tous !
J'ai un petit problème sur un sujet qui m'était pourtant familier au lycée mais que j'ai malheureusement oublié...
Je mets en photo le sujet de ma question, car cela sera plus simple pour la compréhension.
Donc, pour ce qui est du raisonnement pour Delta U, cela ne pose pas de problème. J'aimerais savoir comment peut-on, avec la fonction dans le cercle rouge, trouver le résultat qui est en ordonnée sur le graphique ? En faisant la dérivée ? Si oui, comment ?
Merci par avance pour votre aide
Thibaut
Modifié en dernier par
Nostra8 le 22 Fév 2019, 17:55, modifié 1 fois.
-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
par Sake » 22 Fév 2019, 17:25
Nostra8 a écrit:Bonjour à tous !
J'ai un petit problème sur un sujet qui mettait pourtant familier au lycée mais que j'ai malheureusement oublié...
Je mets en photo le sujet de ma question, car cela sera plus simple pour la compréhension.
Donc, pour ce qui est du raisonnement pour Delta U, cela ne pose pas de problème. J'aimerais savoir comment peut-on, avec la fonction dans le cercle rouge, trouver le résultat qui est en ordonnée sur le graphique ? En faisant la dérivée ? Si oui, comment ?
Merci par avance pour votre aide
Thibaut
Bonjour Nostra8
Où se trouve la photo?
-
Nostra8
- Messages: 6
- Enregistré le: 22 Fév 2019, 16:45
-
par Nostra8 » 22 Fév 2019, 17:48
J'essaie de la joindre mais pas moyen ... Je vais essayer une autre méthode rapidement !
-
mathelot
par mathelot » 22 Fév 2019, 17:52
Nostra8 a écrit:J'essaie de la joindre mais pas moyen ... Je vais essayer une autre méthode rapidement !
tu peux charger le document ici:
http://www.noelshack.com/puis mettre un lien sur maths-forum vers le document.
-
Nostra8
- Messages: 6
- Enregistré le: 22 Fév 2019, 16:45
-
par Nostra8 » 22 Fév 2019, 17:57
D'accord, merci beaucoup !
Donc voici la photo dans le lien ci-dessous:
-
mathelot
par mathelot » 22 Fév 2019, 18:38
bonsoir Thibaut,
je pars de la relation
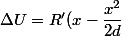I)
La dérivée de
, relativement à x, vaut:
'(x)=R'(1-\frac{x}{d})I)
le nombre dérivé en x=0 vaut:
'(0)=R'I)
l'équation de la tangente T à l'origine est:
 \in T \Leftrightarrow y=R'Ix)
Le point de la tangente d'ordonnée
a pour abscisse:
-
Nostra8
- Messages: 6
- Enregistré le: 22 Fév 2019, 16:45
-
par Nostra8 » 22 Fév 2019, 19:08
D'accord, merci pour la réponse.
Je comprends bien tout le raisonnement. Par contre, justement la valeur qu'il y a en ordonnée, je ne la connais pas à la base et je dois la trouver avec la relation plus haut et c'est la que se pose le problème pour moi
-
mathelot
par mathelot » 22 Fév 2019, 19:27
Nostra8 a écrit: la valeur qu'il y a en ordonnée, je ne la connais pas à la base et je dois la trouver avec la relation plus haut
Le mot-clé est "détermination de la forme canonique du trinôme du second degré".
)
)
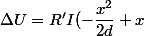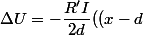^2-d^2))
car
est le début du développement de
^2)
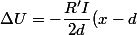^2+\dfrac{R'Id}{2})
L'ordonnée du maximum est
(il s'agit bien d'un maximum car l'axe des ordonnées est orienté vers le bas)
-
Nostra8
- Messages: 6
- Enregistré le: 22 Fév 2019, 16:45
-
par Nostra8 » 23 Fév 2019, 01:08
Hola !!
D'accord, j'ai bien compris le raisonnement mais je n'aurais jamais réussi par moi même ! ^^
Merci beaucoup en tout cas !
Bonne soirée
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
