Bonjour, pourriez-vous m’aider à déterminer les primitives de (x^4+x^3-1)/(x^3+x^2+x) svp
Merci
Primitive
8 messages
- Page 1 sur 1
Re: Primitive
C'est vraiment l'application bébête du cours :
1) division euclidienne :
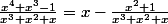
2) décomposition en éléments simples de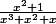
1) division euclidienne :
2) décomposition en éléments simples de
Re: Primitive
D’accord du coup si j’ai bien compris pour le 2) je fait:
f(x)=(ax+b)/x^3+x^2+x et je cherche a et b?
f(x)=(ax+b)/x^3+x^2+x et je cherche a et b?
Re: Primitive
Salut,
Non plutôt ainsi :
(x²+1)/(x³+x²+x) = (x²+1)/[x.(x²+x+1)] = A/x + B/(x²+x+1)
Chercher A et B et ...

Non plutôt ainsi :
(x²+1)/(x³+x²+x) = (x²+1)/[x.(x²+x+1)] = A/x + B/(x²+x+1)
Chercher A et B et ...
Re: Primitive
OnePunchMan a écrit:Oui effectivement c’est mieux
Plutôt :
car
Re: Primitive
Effectivement ça sautait aux yeux (encore fallait-ils les avoir ouverts !)
Mais pour OnePunchMan qui hésite sur la méthode de décomposition en éléments simples peut- être le calcul classique est plus formateur ...
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
