Bonjour,
j'ai besoin d'aide pour cet exercices ( juste des idées ou pistes probables)
Soit f R-->R tq f(x+y)=f(x)+f(y) ( x et y dans R)
On pose a=f(1)
1/ Montrer que pour tout x dans Q, f(x)=ax
2/ On suppose f bornéé au v(0) montrer que pour tout x dans R f(x)=ax
EQUATION FONCTIONELLE
8 messages
- Page 1 sur 1
Re: EQUATION FONCTIONELLE
bonjour,
n désigne un entier naturel.
on commence par calculer f(0).
puis on calcule f(n) , par récurrence sur l'entier n.
puis calculer f(-n).
puis, si p est un entier relatif et q un entier naturel
calculer) en calculant
en calculant =f(q \times \frac{p}{q}))
n désigne un entier naturel.
on commence par calculer f(0).
puis on calcule f(n) , par récurrence sur l'entier n.
puis calculer f(-n).
puis, si p est un entier relatif et q un entier naturel
calculer
Re: EQUATION FONCTIONELLE
mais on ne peut pas calculer f(p) par la formule obtenue par recurrence puisqu'elle est juste seulement pour les elements de N
Re: EQUATION FONCTIONELLE
Aleatoire a écrit:mais on ne peut pas calculer f(p) par la formule obtenue par recurrence puisqu'elle est juste seulement pour les elements de N
entretemps, on calcule f(-n) où n est un entier naturel. comme ça, on a la formule pour tout n dans
Re: EQUATION FONCTIONELLE
tu en es où ? as tu calculé f(0) ?
pour calculer f(-n), écrire de deux façons
f(n+(-n))
pour calculer f(-n), écrire de deux façons
f(n+(-n))
Re: EQUATION FONCTIONELLE
soit 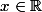 ,
, 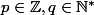
on va montrer que=\frac{p}{q} f(x)) , i.e, que f est
, i.e, que f est  -linéaire.
-linéaire.
=f (px)=p f(x)=q f(\frac{p}{q} x))
d'où
= f(\frac{p}{q} x))
écrivons que f est bornée au voisinage de 0 (zéro):
 tels que
tels que
|< M)
quitte à prendre un alpha plus petit et un M plus grand, on peut supposer que et
et 
sont des rationnels.
Comme f est Q-linéaire,pour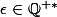
|< \epsilon)
posons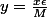
soit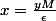
|< \epsilon)
en revenant à la notation "x"
|< \epsilon) (*)
(*)
Soit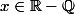
il existe une suite de rationnels) de limite x.
de limite x.
on a l'inégalité
-ax| \leq |f(x)-f(r_n)|+|f(r_n)-ax|)
-ax| \leq |f(x-r_n)|+|a||r_n-x|)
d'après l'inégalité (*):
|< \epsilon) (*)
(*)
pour n assez grand,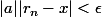
donc pour n assez grand
-ax| \leq 2 \epsilon)
donc pour tout x réel,
f(x)=ax
on va montrer que
d'où
écrivons que f est bornée au voisinage de 0 (zéro):
quitte à prendre un alpha plus petit et un M plus grand, on peut supposer que
sont des rationnels.
Comme f est Q-linéaire,pour
posons
soit
en revenant à la notation "x"
Soit
il existe une suite de rationnels
on a l'inégalité
d'après l'inégalité (*):
pour n assez grand,
donc pour n assez grand
donc pour tout x réel,
f(x)=ax
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 168 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
