Démonstration

[Helenedupain]

Démontrer que :

Bonjours s'il-vous-plaît pouvez-vous m'aider à démontré ceci

[Ben314]

Salut,
1) Prendre le logarithme népérien des trois termes de l'inéquation et la réécrire sous la forme d'un encadrement de ln(n!).
2) Constater que ln(n!)=ln(1)+ln(2)+ln(3)+ . . . + ln(n) est relativement proche [1] de l'intégrale de t=1 à t=n de ln(t)dt [2] et encadrer au mieux l'écart entre les deux pour conclure [3].

[1] Faire un dessin pour voir pourquoi.
[2] Voire éventuellement de l'intégrale de t=3/2 à t=n+1/2 pour plus de précision.
[3] Vu que j'ai rien calculé, c'est là que je sais pas s'il faut être "redoutablement précis" ou si "pas trop précis" ça suffit.

EDIT : En regardant de plus près (et sauf erreur), l'encadrement basique est suffisant pour conclure.

[Helenedupain]

Tout l'exercice c'était ça
1. Demontrer que :

En déduire que :

2. Démontrer que :

J'suis prévenu à faire la première question sans utiliser les intégrales
Je me demande si ça serait possible de les faire la 2em question sans utiliser les intégrales

[Ben314]

Le "sans utiliser les intégrales" est un peu gonflé vu que je suppose que pour montrer le résultat, ben tu as dérivée des fonctions puis, partant de résultat concernant les dérivées en question, tu en a déduit des choses concernant les fonctions elle même. Et bien évidement ce type de raisonnement, c'est de l'intégration.
Certes, on peut parfaitement savoir que [ f'>0 => f croissante ] sans savoir que c'est un résultat d'intégration, mais c'est quand même pas plus con de savoir que c'en est un.

Sinon, le 2), en partant du 1) [comme demandé par le "en déduire que"] c'est immédiat :

Et il suffit de prendre les exponentielle des 3 termes pour conclure (en précisant bien sûr que c'est licite vu que la fonction exponentielle est strictement croissante).

Et pour le 3), tu écrit l'inégalité du 2) pour x=1 ; pour x=2 ; pour x=3 ; . . . ; pour x=n puis tu fait le produit des inégalités et ça donne le résultat demandé (ou alors tu procède par récurrence en utilisant la 2) pour l'hérédité ce qui bien évidement revient exactement au même)

[Helenedupain]

Ah merci beaucoup j'ai réussi à le démontré en faisant le produit membre à menbre des inégalités pour x=1 x=2 x=2 x=n

[Helenedupain]

J'ai utilisé ce genre de méthode pour démontrer les inégalités de la question 1


donc f'(x) <0 la fonction f est strictement décroissante sur pour tout x>0


Donc pour tout x>0 f(x)<0

Pour la deuxième inégalités

j'ai tout tenté pour lever l'indetermination j'ai pas pu
Pouvez vous me montrerez comment es possible en utilisant les intégrales ? J'aimerais bien connaître plusieurs méthodes

[rcompany]

Pour l'inégalité de gauche: poser la suite et montrer par récurrence que :


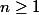montrer que pour on a

On aura alors , équivalent à

Même procédé pour l'inégalité de droite.

[Helenedupain]

Merci beaucoup je comprends mieux la méthode de la récurrence
J'aimerais bien comprendre aussi la méthode avec les intégrales

[Ben314]

Pour t'expliquer la méthode des intégrales et que tu ait l'impression qu'elle "ait du sens", il faut reprendre ton premier post où tu demandais de montrer ça :

Sans préciser que tu avait des questions préliminaires (qu'il fallait sans doute utiliser)
Dans ce truc là, vu qu'il y a le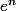 et des puissance variables de partout, ça vient forcément à l'esprit de prendre le logarithme qui simplifie presque tout sauf un truc qu'à priori ça rend pas vraiment plus simple, à savoir les factorielles. Donc le truc chiant c'est les factorielles et on a intérêt à "les isoler" pour mieux voir le bidule (i.e. le voir sous la forme d'un truc un peu compliqué qu'on doit encadrer par des trucs assez simples). Bref, on écrit

Et là, pour montrer que c'est vrai, il faut se poser la question de savoir comment encadrer ?
Et si on revient à la définition de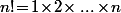 (vu qu'il y a pas grand chose d'autre à faire), on a et là, il y a un outil "standard", c'est de comparer une somme avec une intégrale.
Sans rentrer dans les généralité, dans le cas présent, la fonction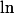 est croissante, donc pour tout on a et, pour tout 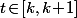on a .
En intégrant, on en déduit que (*).
Puis en sommant (de 2 à à gauche et de 1 à à droite) on obtient .
Et vu qu'une primitive de est , ça donne un encadrement de qui permet de montrer facilement le résultat.

(*) Tape "comparaison somme/intégrale" sur ton moteur de recherche préféré pour voir des tas de dessin expliquant que cet encadrement est totalement trivial graphiquement parlant.

[rcompany]

As-tu déjà étudié les séries de Riemann (approximation d'une intégrale par une série)?

[Helenedupain]

Pour l'inégalité de gauche: poser la suite et montrer par récurrence que :


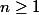montrer que pour on a
es que la ça suffirait pour conclure que c'est vrai au rang n+1?
J'essaie de reprendre ça

[Ben314]

Pour la deuxième inégalités

j'ai tout tenté pour lever l'indetermination j'ai pas pu

Sinon, concernant ça, ben pour montrer la deuxième inégalité, ben faut évidement procéder comme pour la première, c'est à dire commencer par dériver pour "virer les logarithmes" puis regarder comment conclure en partant de l'expression de la dérivée de g.
Ici, g est bien dérivable sur ]0,+oo[ et, sur cet intervalle, vu que , on a donc est décroissante.
Or la limite de en +oo est 0-ln(1)=0 donc g(x)>0 sur ]0,+oo[ (et tu as rien à f... de la limite en 0+ de g qui en fait est égale à +oo)

[Helenedupain]

[quote="Helenedupain"]Tout l'exercice c'était ça
1. Demontrer que :

En déduire que :

2. Démontrer que :

Je parle de cette question la question 2 sans utiliser les intégrales

[Ben314]

Ben ça tu avait dit çi dessus que tu l'avait déjà fait :

Ah merci beaucoup j'ai réussi à le démontrer en faisant le produit membre à membre des inégalités pour x=1 x=2 x=3 . . . x=n