Factorisation de polynômes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Paulygone
- Membre Naturel
- Messages: 11
- Enregistré le: 11 Nov 2018, 23:08
-
 par Paulygone » 17 Nov 2018, 18:07
par Paulygone » 17 Nov 2018, 18:07
Bonjour

J'ai encore un exercice qui me pose problème x)
"Déterminer les réels a et b tels que le polynôme

soit factorisable par
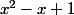
"
Au début je me suis dit qu'il fallait faire comme à l'exercice précédent où il suffisait de trouver les racines du trinôme par lequel on devait factoriser, remplacer x par les racines et trouver les coefficients avec un système de deux équation à deux inconnues. Sauf que là le trinôme n'a pas de racines réelles, du coup je suis un peu perdu ^^'
Merci d'avance pour votre aide

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 17 Nov 2018, 18:15
par Sa Majesté » 17 Nov 2018, 18:15
Salut,
Le polynôme

est factorisable par
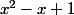
ssi il existe un polynôme P tel que
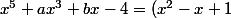 P(x))
.
Trouve le degré de P, écris-le avec des coefficients qui seront tes inconnues, développe et identifie.
-
Paulygone
- Membre Naturel
- Messages: 11
- Enregistré le: 11 Nov 2018, 23:08
-
 par Paulygone » 17 Nov 2018, 18:35
par Paulygone » 17 Nov 2018, 18:35
D'accord merci beaucoup =)
-
Black Jack
 par Black Jack » 17 Nov 2018, 19:19
par Black Jack » 17 Nov 2018, 19:19
Salut,
Alternative :
Faire la division euclidienne de (x^5 + a.x³ + bx - 4) par (x² - x + 1)
Et exprimer que le reste doit être nul.
Sauf erreur, le reste trouvé ici est : (b-1).x - a- 3
Il faut alors que (b-1).x - a - 3 = 0 pour tout x de R et donc ...
Pour cette manière de faire, il faudrait que la division euclidienne mentionnée ici soit encore au programme ...
Et je n'en sais rien.

-
mathelot
 par mathelot » 18 Nov 2018, 01:22
par mathelot » 18 Nov 2018, 01:22
bonjour,
écris que les deux racines complexes de
=x^2-x+1)
sont racines de P (avec
=x^5+ax^3+bx-4)
)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
