Factorisation de polynomes

par **cedricMENTON** » 04 Nov 2007, 13:56

Salut à tous,
Voilà, j'ais un polynomes :

xpuissance 4 + x cube - 4x² + x + 1

je dois le factoriser pour avoir un polinomes du second degrés qui ressemble à ça :

4u² - 2 u + 3

avec u = 3x + 1/x

Mais j'arrive pas à trouver la factorisation....

Aider moi svp !!!!

Merci

par **Quidam** » 04 Nov 2007, 13:58

cedricMENTON a écrit:Salut à tous,
Voilà, j'ais un polynomes :

xpuissance 4 + x cube - 4x² + x + 1

je dois le factoriser pour avoir un polinomes du second degrés qui ressemble à ça :

4u² - 2 u + 3

avec u = 3x + 1/x

Ce ne serait pas plutôt : avec u = x + 1/x ?

par **cedricMENTON** » 04 Nov 2007, 14:22

oui peu importe... c'était juste un exemple comme ça...

par **cedricMENTON** » 04 Nov 2007, 15:29

S'il vous plait je ne comprend vraiment pas

par **Quidam** » 04 Nov 2007, 17:52

cedricMENTON a écrit:oui peu importe... c'était juste un exemple comme ça...

Si, cela importe beaucoup ! Si tu utilises u=3x+1/x ça ne marchera pas !

En posant u=x+1/x, calcule u².
Ensuite mets x² en facteur dans l'équation, et réfléchis un peu : peux-tu remplacer tous les x et les remplacer par des expressions fonction de u ?

par **cedricMENTON** » 04 Nov 2007, 19:49

nan mais ç'est pas ça que je veut dire... Quand je disais 3X+1/X c'était un exemple... je ne sais pas combien vaut "u" et j'arrive pas à le trouver....

par **Quidam** » 04 Nov 2007, 20:22

cedricMENTON a écrit:nan mais ç'est pas ça que je veut dire... Quand je disais 3X+1/X c'était un exemple... je ne sais pas combien vaut "u" et j'arrive pas à le trouver....

Bon, j'abandonne ! Donne-moi le texte exact de ton exercice ! Après on pourra discuter !

par **cedricMENTON** » 04 Nov 2007, 21:12

Ok bon c'est assez long....

On veut résoudre dans R l'équation (E) :

2X^4 - 9X^3 + 14X² - 9X + 2

a) Vérifier que 0 n'est pas solution et établir que l'équation (E) équivaut à l'équation (E1) :

2(x²+1/x²)-9(x+1/x)+14 = 0

b) On pose u = x + 1/x. Calculer u².

Etablir que l'équation (E1) équivaut à :

On donne u=x+1/x

2u²-9u+10=0

c) Résoudre dans R l'équation 2u²-9u+10 = 0

En déduire les solutions de l'équation (E).

d) Adapter la méthode pour résoudre :

x^4+x^3-4x²+x+1 = 0

Alors, j'ais fait la a), la b), la c). J'ais trouvé comme solution 0.5 , 1 , 2

Mais voilà, pour la d), j'arrive pas à trouver une équation de la forme de 2u²-9u+10=0 ni à trouver combien vaut u....

Voilà....

C'est tout....

Merci

par **Quidam** » 04 Nov 2007, 21:36

Eh bien voila ! Mais tu as su tout faire pour la première équation !

Pour la deuxième, c'est exactement pareil.

Je suppose qu'avec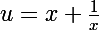

, tu as trouvé que

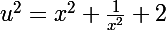et par conséquent que :

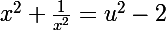
Donc, en partant de

et en remarquant que 0 n'est pas solution, on factorise par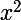

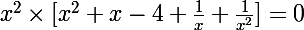
Donc :

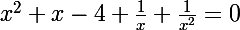
On regroupe :

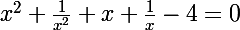
Et là on remplace :

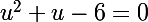
Tu n'as plus qu'à résoudre : tu trouveras deux solutions

et

et ensuite tu n'auras plus qu'à résoudre les deux équations :

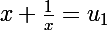
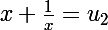
qui se ramèneront à des équations du second degré, ce qui te fera 4 solutions (au maximum : l'une des deux équations, éventuellement les deux, peuvent n'avoir pas de solutions), éventuellement confondues !

par **cedricMENTON** » 04 Nov 2007, 22:01

un seul mot :

MERCIIIII !!!

par **Quidam** » 04 Nov 2007, 22:21

cedricMENTON a écrit:un seul mot :

MERCIIIII !!!

C'était un plaisir ! Je suis bien content que tu ais compris !

Factorisation de polynomes

Factorisation de polynomes

Qui est en ligne