Calcul intégrales

[Palomastoze]

Bonjour, je n'arrive pas à poursuivre mon calcul pour la question 3, en effet je remplace par et j'obtiens :



Cependant je ne vois pas comment poursuivre pour obtenir l'égalité du 3). Voila l'énoncé :



Merci de votre aide

[Ben314]

Salut,
C'est zéro clair ton truc :
Tu écrit que "tu obtient" je sais pas quoi en ne précisant pas d'où tu est parti pour obtenir ta formule.
Donc comment veut tu qu'on te dise si c'est juste ou pas ????

Perso, pour montrer le résultat demandé, j'écrirais les deux intégrales "de même bornes" d'un coté et j'essayerais d'obtenir le résultat demandé. C'est à dire :

En me disant que, bien évidement, il va falloir faire un changement de variable à un moment ou un autre pour changer les bornes de l'intégrale (et peut-être aussi couper en )

[Palomastoze]

Alors j'ai bien mit les intégrales de même borne du même coté puis j'ai séparé pour faire apparaite "0" au niveau des bornes. Ainsi pour les intégrales de 0 à/2 j'ai enlevé la valeur absolu car positif, ce qui donne :



Je me retrouve cependant avec cela, sans pouvoir simplifier d'avantage avant d'appliquer un changement de variable

[Ben314]

Si, tu peut encore grandement simplifier vu que tout ce que tu intègre, c'est des fonctions paires ou impaires donc on remplace aisément les par des .

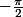
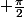
Bon, sinon, j'ai toujours pas fait le moindre calcul de mon coté, mais en regardant quand même "un peu dans le brouillard" le résultat demandé, ça me semble plus que beaucoup louche : la fonction est clairement impaire, donc aussi donc son intégrale de à est nulle. Ce qui rend la formule à démontrer on ne peut plus suspecte.

Je vais faire le calcul, mais à priori, je pense que c'est plutôt qu'il faut intégrer.

Edit : Effectivement, la formule est correcte à condition de prendre le en valeur absolue et de mettre un + à la place du - entre les deux intégrales de droite.
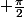
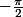
Ou alors, tu garde le - entre les deux et le sans valeur absolue, mais dans ce cas, il faut mettre un coeff. 2 devant l'intégrale et surtout n'intégrer que de 0 à et pas de à
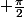
Sans valeur absolue et avec un - , le résultat est faux.

[Palomastoze]

Eh bien en effet j’ai réussi mais seulement en mettant en valeur absolue, ça semble bizarre qu’il y ait une erreur mais bon ! Merci