Aire d'un trapèze

[flo54600]

Bonjour, j'aurais besoin d'aide pour résoudre une énigme que j'ai trouvée sur Internet :

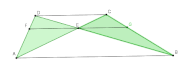
ABCD est un trapèze dont les diagonales se coupent en E.

Les aires des triangles ABE et CDE valent respectivement 32 cm² et 18 cm².

Quelle est l’aire totale du trapèze ABCD ?



J'ai un peu avancé, j'ai pu démontrer que les deux triangles CEA et CEB étaient semblables (utiliser théorème du papillion).

Ensuite, toujours avec le théorème du papillion, on peut calculer k le rapport d'agrandissement grâce à la formule suivante : k²=Aire(EAB) / Aire(EDC) d'où k = Rac (Aire(EAB) / Aire(EDC))

C'est aprés que je n'y arrive pas. Je ne vois pas comment exprimer l'aire de l'un des triangles qui sont semblables (DEA ou CEB)

[aviateur]

Bonjour
On en apprend tous les jours! je n'avais jamais entendu parler du théorème du papillon ainsi que cette nouvelle orthographe de ce Lepidoptera. C'est pour quand le théorème du moustique?
Bref tu peux toujours utiliser tes triangles semblables mais à la base il s'agit tu théorème de Thalès que l'on utilise. Je ne vais pas faire un dessin mais tu imagines une hauteur du trapèze, plus précisément celle qui passe
par E. Le pied cette hauteur qui est sur [CD] je l'appelle F et celui qui est sur [AB] je l'appelle G.
Je pose
Bien sûr on a (1) et l'aire du trapèze c'est:

On utilise le théorème de Thalès (ou tes triangles semblables) pour obtenir
que (2) Le reste ce n'est que de l'arithmétique: on a
(3) et (4)

Là je n'ai pas cherché à être astucieux mais tu prends les 4 équations (1) (2) (3) et (4),
une à la fois et tu élimine une inconnue à la fois pour remplacer à la fin dans A_T.

[hdci]

Que signifie "triangles semblables" ? Les triangles et ne sont sûrement pas proportionnels.
Par contre ils ont la même aire, car en utilisant les hauteurs tombant sur puis en remarquant que

• 
• 

[aviateur]

Bon maintenant on peut aussi repartir de ton rapport d'aire.
Soit a_1=18 (la + petite aire) et l'autre
tu as

Donc

Puis
Cela nous fait une belle formule, il reste à remplacer et par leur valeur.
Cette deuxième façon de faire et plus dans l'esprit de la façon où tu as démarré.

[danyL]

c'est joli
http://therese.eveilleau.pagesperso-ora ... illon.html

[aviateur]

Bonjour
J'aurai pensé à l'effet papillon qui est surement mieux connu https://www.caminteresse.fr/environnement/quest-ce-que-leffet-papillon-1163580/

[flo54600]

Merci pour toutes ces explications, je trouve bien le bon résultat à la fin (98cm²).

Néanmoins j'ai quand même une question.

Dans votre première façon d'opérer, pourquoi votre deuxième équation est : h1/b = h2/B' ?

J'ai vu que h1/b = h2/B' = b / B' = h1/h2 = k , avec k le rapport d'agrandissement que j'avais calculé auparavant et qui vaut Rac ( 18/32).

Or, je ne vois pas pourquoi h1/b = k.

Et oui désolé pour mon fameux théorème du papillon il est préférable de parler du théorème de Thalès avec la configuration dite "papillon".

[flo54600]

Bon maintenant on peut aussi repartir de ton rapport d'aire.
Soit a_1=18 (la + petite aire) et l'autre
tu as

Donc

Puis
Cela nous fait une belle formule, il reste à remplacer et par leur valeur.
Cette deuxième façon de faire et plus dans l'esprit de la façon où tu as démarré.

J'avoue avoir du mal avec la deuxième méthode que vous proposez mais j'aimerais quand même comprendre...

Je bloque au moment où vous passez de

à .

Pouvez-vous juste me détaillez cette étape svp ?

[chan79]

Salut

Une autre approche:
La parallèle à (AB) passant par E coupe [BC] et [DA] en G et F.
On montre facilement avec Thalès que E est le milieu de [FG], pour n'importe quel trapèze.
EFD et EGC ont donc la même aire, de même que EFA et EGB.
Finalement, ADE et BCE ont la même aire x.
Des triangles de même hauteur ayant des aires proportionnelles aux bases, on a 18/x=x/32
donc x=24
L'aire du trapèze est 24+24+18+32=98
On généralise facilement et on retombe sur la formule donnée par aviateur:
Si ABE et CDE ont comme aires et , l'aire de ABCD est

[aviateur]

Bonjour
Merci @chan c'est toujours intéressant d'avoir différentes réponses d'autant plus que @flo54600 semble s'y intéresser.
D'autre part @flo54600 tu n'a pas à t'excuser c'est simplement une boutade que j'ai lancé car effectivement je n'avais jamais entendu parle de ce théorème et j'ai même vérifié il est sur Wikipédia.
Maintenant je répond à tes questions:
Le fait que (=k au passage) c'est le théorème de Thalés ou même simplement ton théorème qui dit simplement que les deux triangles sont semblables.
donc quand tu as affirmé que les
EDC et EAB sont semblables. Mais tu peux dire la même chose pour les triangles EFD et EBG ainsi que ECF et EAG
Donc tu as et et ces deux égalités impliquent
Mais plus simplement
est la hauteur du "petit triangle" et celle du grand triangle.
Donc

Pour la deuxième question j'ai par exemple et je veux faire apparaître il suffit de multiplier par

[flo54600]

Bonjour
Merci @chan c'est toujours intéressant d'avoir différentes réponses d'autant plus que @flo54600 semble s'y intéresser.
D'autre part @flo54600 tu n'a pas à t'excuser c'est simplement une boutade que j'ai lancé car effectivement je n'avais jamais entendu parle de ce théorème et j'ai même vérifié il est sur Wikipédia.
Maintenant je répond à tes questions:
Le fait que (=k au passage) c'est le théorème de Thalés ou même simplement ton théorème qui dit simplement que les deux triangles sont semblables.
donc quand tu as affirmé que les
EDC et EAB sont semblables. Mais tu peux dire la même chose pour les triangles EFD et EBG ainsi que ECF et EAG
Donc tu as et et ces deux égalités impliquent
Mais plus simplement
est la hauteur du "petit triangle" et celle du grand triangle.
Donc

Pour la deuxième question j'ai par exemple et je veux faire apparaître il suffit de multiplier par

Merci beaucoup pour toutes vos explications, j'ai bien compris vos deux méthodes !

[flo54600]

Salut

Une autre approche:
La parallèle à (AB) passant par E coupe [BC] et [DA] en G et F.
On montre facilement avec Thalès que E est le milieu de [FG], pour n'importe quel trapèze.
EFD et EGC ont donc la même aire, de même que EFA et EGB.
Finalement, ADE et BCE ont la même aire x.
Des triangles de même hauteur ayant des aires proportionnelles aux bases, on a 18/x=x/32
donc x=24
L'aire du trapèze est 24+24+18+32=98
On généralise facilement et on retombe sur la formule donnée par aviateur:
Si ABE et CDE ont comme aires et , l'aire de ABCD est

Salut, merci de proposer une autre approche. Je l'ai bien comprise dans l'ensemble. J'ai juste du mal à démontrer que E est le milieu de [FG], pouvez vous m'en dire un peu plus pour cette étape svp ??

[aviateur]

Encore une fois cela vient du théorème de Thalès appliqué aux triangles ACD et BCD
qui ont au demeurant une base commune CD. Donc si on écrit les rapports égaux en simplifiant par CD on trouve que EF=EG

[chan79]

avec Thalès donc
AF/AD=BG/BC
AF/AD=FE/DC
BG/BC=EG/DC
Ca te donne FE=EG

[flo54600]

Et bien merci à vous deux ! J'ai (enfin) tout compris.

[mathelot]

une autre méthode (merci à @hdci):
on note l'aire du triangle ABC

Les deux triangles ayant même base et même hauteur:


d'où


les quotients de longueurs étant égaux aux quotients d'aires














l'aire du trapèze vaut donc:
cm

[flo54600]

@aviateur j'ai finalement une incompréhension en ce qui concerne votre première méthode. Enfin c'est la même question que je vous ai posé ce matin, et je pensais avoir compris mais finalement la réponse que vous m'avez apportée n'était pas celle que j'attendais...
Dans votre première méthode, vous m'avez donné différentes équations qui pourraient m'aider dont la suivante :
(2) : c'est cette équation que je ne comprends pas. Plus précisément, le théorème de Thalès me dit que mais je n'arrive pas à comprendre pourquoi . Je me doute que les rapports sont égaux mais je ne comprends pas pourquoi ils valent forcément k. C'est probablement simple à comprendre mais il y a quelque chose qui m'échappe

[aviateur]

Attention mais n'a aucune raison d'être égal à k. Si je l'ai écrit c'est surement une faute de recopiage. Mais c'est sûr que j'ai utilisé cette égalité mais surement pas que c'est égal à k.