Développement limité d'une expression

[onemorePascal]

Bonjour,

Je bloque sur la solution donnée à un exercice extrait du livre "Introduction à la thermodynamique" (Vuibert).
Il s'agit du 4.3 (p227) réponse 2 : " Il est loisible d'écrire que pv = RT/(1-b/v)-a/v. En faisant un développement limité de cette expression, il vient pv =RT(1+b/v+(b/v)²+(b/v)³+...)-a/v "
Je confirme - pour avoir tracé les 2 courbes sous Excel - que effectivement 1/(1-b/v) ≈ 1+b/v+(b/v)²+(b/v)³+... lorsque b<<v.
Je m'arrache la tête depuis 2 jours pour trouver le détail des calculs intermédiaires (sur papier & sur Internet) pour comprendre et être capable ensuite de faire les autres calculs ailleurs dans le bouquin, sans succès...

Wikipédia donne la définition suivante : "En physique et en mathématiques, un développement limité (noté DL) d'une fonction en un point est une approximation par une fonction polynomiale de cette fonction au voisinage de ce point, c'est-à-dire..."
Il est clairement question d'un point particulier, et non pas d'une superposition complète des 2 courbes comme c'est cas dans mon problème ?! Idem avec la formule de Taylor-Young, toujours au voisinage d'un point de ce que j'en ai vu.

Alors quelqu'un peut-il m'expliquer le calcul d'un développement limité conduisant non pas à avoir une approximation en 1 point seulement, mais bien une fonction polynomiale qui se superpose parfaitement lorsque b<<v.

Merci d'avance.

[pascal16]

1/(1-x) = 1+x+x²+x³ ....
->vient de la limite en +oo de la somme des termes d'une suite géométrique
-> on peut même écrire une égalité avec cette méthode


RT/(1-b/v)

on pose x= b/v
b/v est supposé 'petit' par rapport à 1 sinon, le DL doit être fait autrement.

[Elias]

Salut,

Wikipédia donne la définition suivante : "En physique et en mathématiques, un développement limité (noté DL) d'une fonction en un point est une approximation par une fonction polynomiale de cette fonction au voisinage de ce point, c'est-à-dire..."
Il est clairement question d'un point particulier, et non pas d'une superposition complète des 2 courbes comme c'est cas dans mon problème ?!

Oui, la définition est bien au voisinage d'un point. Mais ici, tu te bloques sur le côté ponctuel "point" mais il y aussi le mot "voisinage à prendre en compte".
Plus précisément, on considère une fonction définie sur un intervalle de . On se donne un point particulier .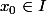
Dire que possède un développement limité d'ordre au point signifie que l'on peut trouver des nombres et une fonction tels que :

pour tout

où vérifie la condition et même


Alors, moralement, ça veut dire que tu peux écrire ta fonction comme la somme d'un polynôme de degré (il s'agit de la partie ) et d'un reste (il s'agit de la partie c'est pour ça que l'on appelle cette fonction comme "reste").

Comme je l'ai souligné, si la fonction a bien envie d'admettre un DL, alors cette égalité est valable pour TOUT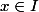 . Mais maintenant, il est pas bête de remarquer que :


- si on prend un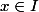 qui est proche de , alors le résultat sera plutôt petit puisque et il sera encore plus petit si l'entier n est grand à cause de la condition [ qui s'interprète en disant que tend beaucoup plus vite vers (lorsque 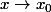) que qui tend bien vite vers 0 quand est grand].
Du coup, les résultats et seront assez proches.



Ainsi, en traçant les courbes et , on aura l'impression que les courbes se superposent sur un intervalle contenant des nombres proches de et ensuite un écart se fera car les seront trop loin de . Cependant, la superposition ne sera pas parfaite mais l'approximation sera de plus en précise lorsque n est grand.


Dans ton cas précis, il s'agit de la fonction suivante (l'intervalle de définition dépend de tes constantes mais bon, pas vraiment grave)



On peut montrer que pour tout, cette fonction admet le DL à l'ordre n au point x_0 = 0 qui a la tête suivante :



avec les mêmes notations que précédemment pour le .
Ca veut dire que si tu prend un assez proche de 0, alors

Du coup,à chaque fois que tu prend un b et v, tu peux écrire que :


Et donc, si tu prend , ça veut dire que b est vraiment petit devant v et donc est assez proche de 0.

Il est donc logique qu'on ait

Et bien sûr, plus n est grand, mieux c'est. Il me semble que tu t'arrêtes à n=3 dans ton poste.

En espérant que ça soit un peu plus clair...

[onemorePascal]

Merci à vous deux Pascal16 et Elias,

C'est vraiment gentil de votre part et je vais maintenant décortiquer ça et voir si je m'en sort avec l'exo suivant, vu que c'est clairement mon but comme précisé dans mon post.

[pascal16]

pour le "assez proche de 0", on un choix assez large, il faut que |x|<1

classique :
si x=1/10 on a x²=1/100 et x³=1/1000

donc le DL donne a peu près 3 chiffres significatif, ça ne sert à rien de garder trop de chiffres significatifs, ils sont faux.

bien :
si x=1/100 on a x²=1/10 000 et x³=1/1 000 000
le DL est là bien plus précis.

pas beau :
x=1/2, ça marche encore, mais il faudra aller jusqu'à x¹° dans le DL pour avoir 3 décimales de précision.

Les gars qui ont pensé des langages fonctionnels avant la seconde guerre mondiale y avaient pensé et la précision du calcul faisait partie de la valuation d'un calcul qui n'avait pas d'expression littérale.