Algèbre: application linéaire
19 messages
- Page 1 sur 1
Algèbre: application linéaire
Bonjour, je suis actuellement bloqué sur une exercice qui pose plusieurs question piège qui demande de donner des exemple d'application linéaire de R 2 -> R 2 qui n'a aucune valeur propre, ou encore une application linéaire de R 2 -> R 2 qui a une valeur propre et qui n'est pas diagonalisable et ces mêmes questions pour R 3 -> R 3
Si je pouvais avoir de l'aide ça sera super merci d'avance!
Si je pouvais avoir de l'aide ça sera super merci d'avance!
Re: Algèbre: application linéaire
Bonjour Barbotte, connais-tu la notion de polynôme caractéristique pour une application linéaire de R^2 dans R^2 ou de R^3 dans R^3?
Cordialement
Cordialement
Re: Algèbre: application linéaire
Oui avec la matrice A - X*(la matrice identité) ?
Mais je ne vois pas en quoi ça m'aiderait a trouver des exemple d'application linéaire qui n'ont pas de valeur propre.
Mais je ne vois pas en quoi ça m'aiderait a trouver des exemple d'application linéaire qui n'ont pas de valeur propre.
Re: Algèbre: application linéaire
Bonjour
Tu peux bien sur suivre la piste qui utilise les polynômes caractéristiques.
Tu peux aussi réfléchir de manière géométrique. Ne connais-tu pas une opération géométrique de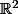 dans lui-même telle que l'image d'un vecteur non nul ne lui soit jamais colinéaire?
dans lui-même telle que l'image d'un vecteur non nul ne lui soit jamais colinéaire?
Tu peux bien sur suivre la piste qui utilise les polynômes caractéristiques.
Tu peux aussi réfléchir de manière géométrique. Ne connais-tu pas une opération géométrique de
Re: Algèbre: application linéaire
Sais tu calculer le polynôme caractéristique de la matrice 
par exemple?
Quel est le lien entre la notion de polynôme caractéristique et la notion de valeur propre? (voir ton cours si tu ne sais pas)
@Mimosa Tout à fait
par exemple?
Quel est le lien entre la notion de polynôme caractéristique et la notion de valeur propre? (voir ton cours si tu ne sais pas)
@Mimosa Tout à fait
Re: Algèbre: application linéaire
Le polynôme de A serait X^2 -1 si je ne me trompe pas ? Donc X=1 et X=-1 seraient les valeurs propre de A, il faut plutôt trouver un polynôme du style X^2 +1 pour qu'il n'y ai pas de solution non ?
Re: Algèbre: application linéaire
Barbotte a écrit:Le polynôme de A serait X^2 -1 si je ne me trompe pas ? Donc X=1 et X=-1 seraient les valeurs propre de A, il faut plutôt trouver un polynôme du style X^2 +1 pour qu'il n'y ai pas de solution non ?
Justement, attention au signe dans ton calcul de déterminant ! Et d'un point de vue géométrique, comme le disait Mimosa, à quelle transformation correspond cette matrice?
Re: Algèbre: application linéaire
Si on remplace un 1 par -1 on a un polynôme du style X^2 +1 donc il faudrait que x^2=-1 donc impossible dans le réel je ne me trompe pas ?
Modifié en dernier par Barbotte le 26 Juin 2018, 17:36, modifié 1 fois.
Re: Algèbre: application linéaire
Et aussi je ne vois pas non plus quelle application linéaire de pourrais pas être diagonalisable alors qu'elles ont une ou deux valeurs propres dans R^2 ou R^3
Re: Algèbre: application linéaire
Barbotte a écrit:Si on remplace un 1 par -1 on a un polynôme du style X^2 +1 donc il faudrait que x^2=1 donc impossible dans le réel je ne me trompe pas ?
Bonjour
Tu veux dire qu'il faudrait que x^2=-1, donc impossible dans le réel ? En effet, la matrice obtenue n'a pas de valeurs propres dans R.
Re: Algèbre: application linéaire
Barbotte a écrit:Et aussi je ne vois pas non plus quelle application linéaire de pourrais pas être diagonalisable alors qu'elles ont une ou deux valeurs propres dans R^2 ou R^3
Dans R2, il faut une application qui a une seule valeur propre double (si elle a 2 valeurs propres distinctes, elle est diagonalisable), mais dont le sous-espace propre associé est de dimension 1.
Que peut-on mettre à la place du "?" pour que l'application linéaire associée à cette matrice soit dans ce cas ?
Re: Algèbre: application linéaire
Oui c'est ce que je voulais dire petite erreur de frappe 
Ah oui bien vu merci bien, il me reste plus que dans R^3
Ah oui bien vu merci bien, il me reste plus que dans R^3
Re: Algèbre: application linéaire
Pseuda a écrit:Barbotte a écrit:Et aussi je ne vois pas non plus quelle application linéaire de pourrais pas être diagonalisable alors qu'elles ont une ou deux valeurs propres dans R^2 ou R^3
Dans R2, il faut une application qui a une seule valeur propre double (si elle a 2 valeurs propres distinctes, elle est diagonalisable), mais dont le sous-espace propre associé est de dimension 1.
Que peut-on mettre à la place du "?" pour que l'application linéaire associée à cette matrice soit dans ce cas ?
un 2 merci je viens de la trouver à l'instant
Re: Algèbre: application linéaire
Barbotte a écrit:Oui c'est ce que je voulais dire petite erreur de frappe
Ah oui bien vu merci bien, il me reste plus que dans R^3
Dans R^3, le polynôme caractéristique est de degré 3, peut-il n'avoir aucune racine ?
Re: Algèbre: application linéaire
Non en effet, un polynôme de degré 3 à coefficients réels a au moins une racine dans R (prends un polynôme de degré 3, limites en + et - l'infini ?, théorème des valeurs intermédiaires).
Les valeurs propres d'une application linéaire de R^n sont les racines dans R de son polynôme caractéristique. Donc, dans R^3, une matrice peut-elle n'avoir aucune valeur propre ?
Les valeurs propres d'une application linéaire de R^n sont les racines dans R de son polynôme caractéristique. Donc, dans R^3, une matrice peut-elle n'avoir aucune valeur propre ?
Re: Algèbre: application linéaire
Rebonjour
Pour finir ce que je voulais dire hier. Dans le cas du plan, il y a une erreur dans la matrice donnée par LB2.
Il s'agit de

dont le polynôme caractéristique est bien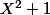 et qui représente la rotation de centre
et qui représente la rotation de centre  et d'angle
et d'angle 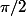 et qui n'a évidemment pas de vecteur propre!
et qui n'a évidemment pas de vecteur propre!
Pour finir ce que je voulais dire hier. Dans le cas du plan, il y a une erreur dans la matrice donnée par LB2.
Il s'agit de
dont le polynôme caractéristique est bien
Re: Algèbre: application linéaire
Mimosa a écrit:Rebonjour
Pour finir ce que je voulais dire hier. Dans le cas du plan, il y a une erreur dans la matrice donnée par LB2.
Il s'agit de
dont le polynôme caractéristique est bienet qui représente la rotation de centre
et d'angle
et qui n'a évidemment pas de vecteur propre!
Oui tout à fait! Merci de la correction
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
