Points critiques

[coco7513]

Bonjour, soit f une fonction de R^3 dans R avec f(x,y,z)=sin(yz-x)+e^(x-yz).

J'ai montré dans un premier temps que tout point (x,y,z) tel que x=yz est un point critique (il suffit de calculer les dérivées partielles et de vérifier le système d'équations...).

Maintenant, pour donner la nature de chacun de ces points, je me suis dit qu'il fallait calculer la matrice Hessienne et j'ai trouvé :

H(f)=(1 -z -y
-z z^2 yz
-y yz y^2)

En calculant le déterminant de cette matrice, je trouve 0. Je pense que je ne suis pas sur la bonne voix... Si quelqu'un peut m'aider....

Merci d'avance pour vos réponse.

[Ben314]

Salut,
C'est pas étonnant que ta fonction soit complètement dégénérée vu qu'en fait, f(x,y,z) ne dépend "pas vraiment" de x,y,z mais uniquement du réel yz-x :
.
Et si tu prend un réel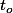 fixé, les éléments tel que c'est tout ceux tels que avec et quelconques donc au voisinage de n'importe quel point il y a forcément des tonnes d'autres points qui donnent la même valeur pour donc évidement la même valeur pour et ça signifie bien sûr que pour tes points critiques, ta Hessienne ne peut jamais être définie positive ou définie négative vu que ça signifierais que tu as un max. ou un min local strict alors que ça ne peut pas exister.

Bref, tu va avoir des max/min locaux non stricts (donc non repérable avec la hessienne qui aura toujours un déterminant nul) et qui vont bêtement correspondre aux différent max/min de la fontion (réelle) (qui a des tas d’extremums locaux, mais qu'on ne sait pas exprimer simplement à part celui en 0).

[coco7513]

Merci pour ta réponse Ben314 mais je ne suis pas sûr d'avoir tout compris mais dans le cours y'a un tas de choses sur les signes des valeurs propres : si les 2 sont <0 c'est un max, si c'est >0 c'est un min et si les 2 sont de signes contraires alors c'est un point selle.

J'ai calculer les valeurs propres de la Hessienne et j'ai trouvé 0 et y^2+z^2+1, c'est vraiment bizarre, il y a rien dans le cours sur les vp égale à 0.

J'ai l'impression de ne pas être sur la bonne voie...