Équation paramétrique de courbes implicites

[Sharkk]

Bonjour, je ne vois pas du tout comment paramétrer une courbe à partir d'une équation comme celle-ci

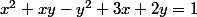
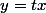
Après avoir cherché sur le net, dans beaucoup de cas il est posé sans trop d'explications, cependant je ne comprends pas d'ou cela vient, et j'ai l'impression que dans ce cas précis cela ne nous aide pas trop car cela m'amène à et donc, il est difficile d'exprimer x en fonction de t à part calculer le discriminant de cette expression, mais je crains d'avance d'avoir quelque chose de pas très joli
Merci d'avance pour votre aide

[Ben314]

Salut,
Tu veut "paramétrer" cette courbe, mais pour faire quoi ?
Là, ta courbe, c'est une conique et plus précisément une hyperbole, donc il y a des tas de façon simple de la paramétrer, et quasiment toutes les méthodes passent par la recherche des "éléments caractéristique" de ta courbe, c'est à dire ici le centre et les asymptotes.

[Kolis]

Bonjour !
Le "truc" suppose que la courbe passe par l'origine, ce qui n'est pas le cas ici.

Comme c'est une conique, toute droite (de coefficient directeur ) passant par un point de la courbe (à toi d'en faire le choix) coupe la conique en deux points (éventuellement un seul) et comme tu en connais un il te reste une équation du premier degré qui te donnera une expression de en fonction de .

Si tu en sais plus sur les coniques (suggestion de Ben314) tu peux aussi "couper" par une droite parallèle à une asymptote : de nouveau une équation de degré 1.