Théorème des fonctions implicites

[klaus2010]

Bonjour,
J'ai lu comme corollaire de théorème des fonctions implicites que:
Soit A une ensemble ouverte dans R^n , M est k * n matrice ces entiers sont
les des fonctions réels lisse définissent sur A, b est k-vecteur ses entiers aussi les valeurs des fonctions réels lisse définissent sur A, supposant que pour tout x_0 de A on a rang M(x_0)=k
Donc il existe une voisinage ouverte U de x_0 et application lisse G de U vers R^n tq M(x)G(x)=b(x) pour tout x dans U.

Le problème est dans le théorème des fonctions implicites , on propose que
la fonction (F par exemple) s'annule dans certains points .. ici c'est pas le cas
vous pouvez m'aidez pour clarifier cette corollaire ?
merci d'avance...

[Ben314]

Salut,
Si j'ai bien compris l'énoncé (ton français est pas encore totalement au "top" niveau), ce qui doit venir à l'esprit si on veut utiliser le théorème des fonctions implicites, c'est d'utiliser la fonction :

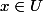Et le problème posé se ramène bien à chercher une fonction telle que, pour tout , on ait .

SAUF QUE :

1) Si kM(x)^(-1) est elle aussi lisse et, bien sûr, pour avoir M(x)G(x)=b(x), il faut prendre G(x)=M(x)^(-1)b(x).

Bon, évidement, il y a aussi la posibilité que j'ai mal compris l'énoncé...

[klaus2010]

merci Ben ! et désolé pour ma langue...

Salut,
Si j'ai bien compris l'énoncé (ton français est pas encore totalement au "top" niveau), ce qui doit venir à l'esprit si on veut utiliser le théorème des fonctions implicites, c'est d'utiliser la fonction :

Et le problème posé se ramène bien à chercher une fonction telle que, pour tout , on ait .

SAUF QUE :

1) Si kM(x)^(-1) est elle aussi lisse et, bien sûr, pour avoir M(x)G(x)=b(x), il faut prendre G(x)=M(x)^(-1)b(x).

Bon, évidement, il y a aussi la posibilité que j'ai mal compris l'énoncé...