bonjour,
je dois montrer qu'une application est injective mais je ne sais pas comment faire...
voilà: f: N² \Rightarrow N
(x;y) \Rightarrow ((x+y)(x+y+1)/2)+y
j'ai considéré deux couples de N² (x;y) et (a;b)
et j'ai supposé qu f((a;b))=f((x;y)) donc b-y= ((x+y)(x+y+1)-(a+b)(a+b+1))/2
enfin arrivée là, je ne sais pas comment montrer que (x+y)(x+y+1)= (a+b)(a+b+1)
et donc montrer que b=y
Injection
12 messages
- Page 1 sur 1
Re: injection
Une façon de faire, peu calculatoire, sans critère de divisibilité ni partie entière (donc pas la plus belle) :
on peut remarquer que (x+y)(x+y+1)/2 =
f(a,b)=f(x,y) devient
(1+2+3+...+(a+b) ) + b = (1+2+3+...+(x+y) ) +y
supposons b>=y , on a alors
b -y = (1+2+3+...+(x+y) ) -(1+2+3+...+(a+b) )
à gauche 0<=b-y <= b, mais à droite, peut-on avoir une différence plus petite que b ? (c'est aussi comme ça que tu peux faire dans ton calcul)
de même pour b<=y, conclusion sur l'égalité au pas de b et y ?
puis sur celle de (a+b) et (x+y)
...
on peut remarquer que (x+y)(x+y+1)/2 =
f(a,b)=f(x,y) devient
(1+2+3+...+(a+b) ) + b = (1+2+3+...+(x+y) ) +y
supposons b>=y , on a alors
b -y = (1+2+3+...+(x+y) ) -(1+2+3+...+(a+b) )
à gauche 0<=b-y <= b, mais à droite, peut-on avoir une différence plus petite que b ? (c'est aussi comme ça que tu peux faire dans ton calcul)
de même pour b<=y, conclusion sur l'égalité au pas de b et y ?
puis sur celle de (a+b) et (x+y)
...
Re: injection
merci beaucoup Pascal16, je commençais à désespérer!
par contre faut-il justifier la remarque ou est-ce que c'est une règle?
par contre faut-il justifier la remarque ou est-ce que c'est une règle?
Re: injection
il faut que tu justifie proprement que (1+2+3+...+(x+y) ) -(1+2+3+...+(a+b) ) ne peut pas être plus petit que b sauf s'ils sont égaux.
on sait que c'est positif
donc laquelle des listes est la plus longue ?
par quoi peut-on la minorer ?
et ensuite il faut justifier que c'est plus grand que b.
[PS] trouve ça et je te donne une version propre
on sait que c'est positif
donc laquelle des listes est la plus longue ?
par quoi peut-on la minorer ?
et ensuite il faut justifier que c'est plus grand que b.
[PS] trouve ça et je te donne une version propre
Re: injection
Salut,
On peut aussi s'en sortir sans la "remarque astucieuse" :
On considère deux couples (a,b) et (x,y) de NxN tels que f(x,y)=f(a,b), c'est à dire tels que
(x\!+\!y\!+\!1)}{2}\!+\!y =\dfrac{(a\!+\!b)(a\!+\!b\!+\!1)}{2}\!+\!b\ (*))
Supposons que (strict).
(strict).
Vu que ce sont des nombres entiers, on a donc (large) et on en déduit que :
(large) et on en déduit que :
(x\!+\!y\!+\!1)}{2}\!+\!y <br />\geq\dfrac{(x\!+\!y)(x\!+\!y\!+\!1)}{2}<br />\geq\dfrac{(a\!+\!b\!+\!1)(a\!+\!b\!+\!2)}{2}<br />=\dfrac{(a\!+\!b\!+\!1)(a\!+\!b)}{2}\!+\!(a\!+\!b\!+\!1)>\dfrac{(a\!+\!b\!+\!1)(a\!+\!b)}{2}\!+\!b)
Ce qui est en contradiction avec l'hypothèse selon laquelle f(x,y)=f(a,b).
Pour des raison de symétrie, l'hypothèse conduit elle aussi à une contradiction donc
conduit elle aussi à une contradiction donc  .
.
L'hypothèse) nous dit alors que
nous dit alors que  et, vu que
et, vu que  , c'est qu'on a aussi
, c'est qu'on a aussi 
On peut aussi s'en sortir sans la "remarque astucieuse" :
On considère deux couples (a,b) et (x,y) de NxN tels que f(x,y)=f(a,b), c'est à dire tels que
Supposons que
Vu que ce sont des nombres entiers, on a donc
Ce qui est en contradiction avec l'hypothèse selon laquelle f(x,y)=f(a,b).
Pour des raison de symétrie, l'hypothèse
L'hypothèse
Modifié en dernier par Ben314 le 22 Nov 2017, 22:45, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: injection
merci Pascal16 mais comme nous n'avons pas encore étudié les listes encore moins leur minorant, alors j'ai utilisé la soustraction, la comparaison des carrés mais ça n'a rien donné donc je ne sais pas comment arriver la contradiction...
quant à Ben314, merci pour la technique sans "la remarque astucieuse" !
quant à Ben314, merci pour la technique sans "la remarque astucieuse" !
Re: injection
Recherche de l'antécédent d'un entier a
soit Sn la suite définie par
Sn est strictement croissante, donc il existe un unique p tel que Sp<= a <Sp+1
cherchons x et y, entiers naturels tels que :
y = a - Sp
x+y = p
(x;y) est l'antécédent de a.
[PS] Sn=n(n+1)/2, p=partie entière (2racine(a)) pour a 'grand'.
soit Sn la suite définie par
Sn est strictement croissante, donc il existe un unique p tel que Sp<= a <Sp+1
cherchons x et y, entiers naturels tels que :
y = a - Sp
x+y = p
(x;y) est l'antécédent de a.
[PS] Sn=n(n+1)/2, p=partie entière (2racine(a)) pour a 'grand'.
Modifié en dernier par pascal16 le 25 Nov 2017, 13:09, modifié 1 fois.
Re: injection
mais nous n'avons même pas étudié les suites donc il ne serait pas correcte de donner une réponse utilisant des connaissances que nous ne sommes pas censés avoir..
Re: injection
salut
Un dessin pour visualiser cette injection de
de 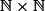 dans
dans  qui est d'ailleurs une bijection.
qui est d'ailleurs une bijection.
Les éléments de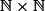 sont numérotés, en rouge, diagonale après diagonale.
sont numérotés, en rouge, diagonale après diagonale.
On visualise et on démontre facilement que:
(x+y+1)}{2}\leq f(x,y)<\frac{(x+y+1)(x+y+2)}{2})
(4+2+1)}{2} \leq f(4,2) < \frac{(4+2+1)(4+2+2)}{2}) soit
soit 
Un dessin pour visualiser cette injection
Les éléments de
On visualise et on démontre facilement que:
- Fichiers joints
-
- injection.gif (12.34 Kio) Vu 573 fois
Re: injection
salut
je rajoute une question:
Trouver le couple d'entiers (a,b) tel que f(a,b)=20172017
je rajoute une question:
Trouver le couple d'entiers (a,b) tel que f(a,b)=20172017
Re: injection
Bonjour
Si on pose n=x+y
On cherche le plus grand entier n tel que n(n+1)/2 <=20172017
c'est à dire tel que n²+n - 40344034 soit négatif
Le delta est positif les solutions sont des signes contraires, il faut donc prendre la partie entière de la solution positive, elle vaut 6351, n =6351.
On a 6351*6352 = 20170776
On en déduit y = 20172017-20170776=1241
et x=n-y=5110
Donc c'est (5110,1241)
Si on pose n=x+y
On cherche le plus grand entier n tel que n(n+1)/2 <=20172017
c'est à dire tel que n²+n - 40344034 soit négatif
Le delta est positif les solutions sont des signes contraires, il faut donc prendre la partie entière de la solution positive, elle vaut 6351, n =6351.
On a 6351*6352 = 20170776
On en déduit y = 20172017-20170776=1241
et x=n-y=5110
Donc c'est (5110,1241)
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 98 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
