Application injective ? surjective?

[Meii]

bon j'ai un petit probléme avec la valeur absolu .. pouvez vous m'aidez ?
Soit f de R vers R défini par f(x)= |2-|x||
f est elle injective? surjective?

[FLBP]

Bonsoir,

Aucun des deux, vu tes ensembles de départ et d'arrivée :

pas injective
pas défini pas surjective

Cordialement.

EDIT: Avec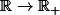 f est surjective

[Meii]

comment je peut le démontrer avec plus de détails.. ?

[FLBP]

Ces deux contres-exemples suffisent.

[pascal16]

la courbe a une forme de W
|x| est en forme de V
-|x| est en forme de V renversé
2-|x| est en forme de V renversé décalé de 2 vers le haut
|2-|x| | est en forme de W
donc il existe de nombres qui ont 2, 3 ou 4 antécédents? -> pas injective.
exemple f(2)=f(-2)=0, donc f non injective (voir ta définition de cours avec les images)
f non surjective : car aucun nombre strictement négatif n'a d'antécédent

[Meii]

Merci beaucoup ^-^