Application injective et surjective

par **MoRBT** » 28 Déc 2011, 22:23

Bonjour,

Je ne trouve pas une solution à ce problème:

Soit E, E', F, F' quatre ensemble,

,

deux applications et

l'application définie par

. Montrer :

a) si

est surjective et

est injective, alors

est injective
b) si

est injective et

est surjective, alors

est surjective

Je vous remercie par avance.

par **girdav** » 29 Déc 2011, 00:01

Pour le a), prend

et

deux applications de

dans

, telles que

, et

dans

.

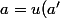pour un certain

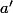
et

. Vois-tu comment poursuivre ?

par **MoRBT** » 29 Déc 2011, 11:01

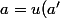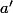
girdav a écrit:Pour le a), prend et deux applications de dans , telles que , et dans . pour un certain et . Vois-tu comment poursuivre ?

Merci Beaucoup girdav,

La suite de la solution devrait être comme ça:

Puisque

est injective alors

donc

Je vous remercie