égalité
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
elchapo93
- Messages: 6
- Enregistré le: 24 Sep 2017, 13:25
-
 par elchapo93 » 24 Sep 2017, 13:29
par elchapo93 » 24 Sep 2017, 13:29
Bonjour à tous!
J'ai quelques soucis à résoudre cette égalité , ça fait très longtemps que j'ai pas fait de maths, donc une âme charitable ne serait pas de refus!

4 x n=52 x (n-2)
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 24 Sep 2017, 13:40
par infernaleur » 24 Sep 2017, 13:40
Pour résoudre une équations du type AX=B(X-C) (on doit trouver X)
on développer d'abord le membre de droite : AX=BX-BC
on fait passer les membres où il y a l'inconnue à gauche et tout le reste à droite: AX-BX=-BC
On a (A-B)X=-BC
Donc X=-BC/(A-B)
à toi d'appliquer ce raisonnement pour trouver n
-
elchapo93
- Messages: 6
- Enregistré le: 24 Sep 2017, 13:25
-
 par elchapo93 » 24 Sep 2017, 13:57
par elchapo93 » 24 Sep 2017, 13:57
Merci,
Si je suis ton raisonnement ça donne :
4n=52 (n-2)
4n=52n-104
4n-52n=-104
(4-52)n=-104
n=-104/(4-52)
Ai-je bon?
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 24 Sep 2017, 14:04
par infernaleur » 24 Sep 2017, 14:04
Oui mais dés la troisième ligne tu aurais pu faire 4n-52n=-48n donc au final n=-104/-48=104/48
-
elchapo93
- Messages: 6
- Enregistré le: 24 Sep 2017, 13:25
-
 par elchapo93 » 24 Sep 2017, 14:27
par elchapo93 » 24 Sep 2017, 14:27
Ok merci beaucoup,
Cependant dans la correction que j'ai (tage mage) , c'est différent, on a :
Soit n le nombre d’amis, le cadeau vaut 44 n (ils paient tous 44 euros) ou alors 52 x (n-2).
Il ne reste plus qu’à résoudre l’égalité : 4 x n=52 x (n-2), pour conclure que n=13,
Est ce une erreur de la correction?
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 24 Sep 2017, 14:36
par infernaleur » 24 Sep 2017, 14:36
résoudre l'égalité 4 x n=52 x (n-2) ne peux pas donner 13 donc oui il y a une erreur.
Tu peux donner l'énoncé complet de la question stp ?
-
elchapo93
- Messages: 6
- Enregistré le: 24 Sep 2017, 13:25
-
 par elchapo93 » 24 Sep 2017, 14:38
par elchapo93 » 24 Sep 2017, 14:38
Voici l'énoncé:
Question 3. Un groupe d’étudiants décide d’acheter un cadeau d’anniversaire à leur ami. Cela leur coûtera
44 euros chacun. Cependant, si deux d’entre eux décide de ne pas payer, cela coutera 52 euros aux
payeurs. Combien coûte le cadeau ?
A) 410 B) 468 C) 518 D) 572 E) 614
-
elchapo93
- Messages: 6
- Enregistré le: 24 Sep 2017, 13:25
-
 par elchapo93 » 24 Sep 2017, 14:38
par elchapo93 » 24 Sep 2017, 14:38
Et voici la réponse:
Réponse D
Soit n le nombre d’amis, le cadeau vaut 44 n (ils paient tous 44 euros) ou alors 52 x (n-2).
Il ne reste plus qu’à résoudre l’égalité : 4 x n=52 x (n-2), pour conclure que n=13, et donc que le cadeau
vaut 572€.
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 24 Sep 2017, 14:45
par infernaleur » 24 Sep 2017, 14:45
Ah bha il ne faut pas résoudre 4 x n=52 x (n-2) mais 44n=52(n-2) !!
Le cadeau leur coutera 44 euros chacun et non 4 euro chacun si tout le monde paye.
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 24 Sep 2017, 14:46
par infernaleur » 24 Sep 2017, 14:46
Comprend-tu pourquoi il faut résoudre cette égalité ? Où tu n'as que regarder la réponse ?
-
elchapo93
- Messages: 6
- Enregistré le: 24 Sep 2017, 13:25
-
 par elchapo93 » 24 Sep 2017, 14:53
par elchapo93 » 24 Sep 2017, 14:53
Oh le gros bêta que je suis, oui je comprends tout à fait, j'avais regardé la correction et du coup j'ai cherché à résoudre l'égalité sans faire attention à l'erreur, merci beaucoup en tout cas!
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 24 Sep 2017, 14:56
par infernaleur » 24 Sep 2017, 14:56
Pas de soucis ^^

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 24 Sep 2017, 18:36
par zygomatique » 24 Sep 2017, 18:36
salut
on peut aussi apprendre les tables de multiplication et se simplifier la vie
il est ""évident"" que 52 est multiple de 4 puisque 52 = 40 + 12
donc
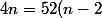 \iff n = 13(n - 2) \iff ...)
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités