Bonjour à tous je m'excuse d'avance je suis débutant dans l'étude des matrices euh je suis bloqué sur une propriété de l'inverse d'une matrice.c'est celle-ci
(AB)−1 = B−1A−1
excusez moi pour moi les -1 ils sont en exposants je ne maîtrise pas encore l'éditeur d'équation
Inverse d'une matrice
2 messages
- Page 1 sur 1
Re: inverse d'une matrice
Salut,
Par définition, l'inverse d'une matrice C (carrée de taille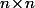 ) c'est la matrice D telle que
) c'est la matrice D telle que  et
et 
Remarques :
- L'inverse peut ne pas exister, mais s'il existe il est unique (ce qui explique le "la matrice D..." de la définition.
- En fait si on a une matrice D telle que alors il est inutile de vérifier que
alors il est inutile de vérifier que  , ça sera forcément vrai. C'est une propriété bien pratique mais difficile à démontrer donc souvent admise au début.
, ça sera forcément vrai. C'est une propriété bien pratique mais difficile à démontrer donc souvent admise au début.
Pour revenir à ton exo.,pour vérifier si c'est vrai ou pas que l'inverse du produit AB c'est une certaine matrice D, que doit on calculer ?
Ou, si tu préfère, si on a le produit AxB, par quoi doit on multiplier (par exemple à droite) pour avoir comme résultat :
: 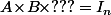
P.S. : Si tu veut faire des maths un peu sérieusement et ne pas (rapidement) raconter de (grosses) connerie, il faut absolument comprendre que ta formule^{-1}=B^{-1}A^{-1}) ne doit jamais être énoncée "tout crue", mais forcément précédé d'un "contexte" (=hypothèses) qui, dans le cas présent, est :
ne doit jamais être énoncée "tout crue", mais forcément précédé d'un "contexte" (=hypothèses) qui, dans le cas présent, est :
Si A et B sont deux matrices inversibles de même taille alors le produit est forcément lui même inversible et on a la formule ...
est forcément lui même inversible et on a la formule ...
Par définition, l'inverse d'une matrice C (carrée de taille
Remarques :
- L'inverse peut ne pas exister, mais s'il existe il est unique (ce qui explique le "la matrice D..." de la définition.
- En fait si on a une matrice D telle que
Pour revenir à ton exo.,pour vérifier si c'est vrai ou pas que l'inverse du produit AB c'est une certaine matrice D, que doit on calculer ?
Ou, si tu préfère, si on a le produit AxB, par quoi doit on multiplier (par exemple à droite) pour avoir comme résultat
P.S. : Si tu veut faire des maths un peu sérieusement et ne pas (rapidement) raconter de (grosses) connerie, il faut absolument comprendre que ta formule
Si A et B sont deux matrices inversibles de même taille alors le produit
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
