Inégalité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 11 Aoû 2017, 13:29
par mehdi-128 » 11 Aoû 2017, 13:29
Bonjour,
Pour tout réels positifs ou nuls a,b pour tout p>1 tel que :

Montrer que :
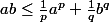
J'ai pas d'idée...
-
NicoTial
- Membre Naturel
- Messages: 81
- Enregistré le: 24 Juil 2017, 12:50
-
 par NicoTial » 11 Aoû 2017, 13:32
par NicoTial » 11 Aoû 2017, 13:32
Tu as plusieurs méthodes :
-la première tu fais une étude de fonction basique n fixant l'un des paramètres comme étant une inconnue.
-la deuxième méthode utilise la convexité (respectivement la concavité) de la fonction exponentielle (respectivement de la fonction logarithme)... Je préfère personnellement utilisé la fonction exponentielle...
Donc a et b étant positifs, tu peux dire qu'ils sont l'image à travers l'exponentielle, de x et y par exemple... essaye de voir avec ça...
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 11 Aoû 2017, 14:19
par mehdi-128 » 11 Aoû 2017, 14:19
L'indication parle d'utiliser le logarithme.
Mais quelle est la propriété utile de la concavité du logarithme à utiliser ?
-
NicoTial
- Membre Naturel
- Messages: 81
- Enregistré le: 24 Juil 2017, 12:50
-
 par NicoTial » 11 Aoû 2017, 14:20
par NicoTial » 11 Aoû 2017, 14:20
quelle est la définition de la concavité ?
-
NicoTial
- Membre Naturel
- Messages: 81
- Enregistré le: 24 Juil 2017, 12:50
-
 par NicoTial » 11 Aoû 2017, 14:23
par NicoTial » 11 Aoû 2017, 14:23
si ta définition est que -f est convexe, alors dit moi ce qu'est une fonction convexe...
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 11 Aoû 2017, 14:51
par mehdi-128 » 11 Aoû 2017, 14:51
On a :
=ln(a)+ln(b)=\frac{1}{p}ln(a^p)+\frac{1}{q}ln(a^q))
Une fonction convexe f c'est :
Pour tout t dans [0,1] :
y) \leq tf(x) + (1-t)f(y))
Je dois prendre
=-ln(x))
?
-
NicoTial
- Membre Naturel
- Messages: 81
- Enregistré le: 24 Juil 2017, 12:50
-
 par NicoTial » 11 Aoû 2017, 14:58
par NicoTial » 11 Aoû 2017, 14:58
oui c'est ça, tu es presque à la conclusion...
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 11 Aoû 2017, 17:22
par mehdi-128 » 11 Aoû 2017, 17:22
On prend :
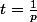
alors
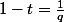
Et :
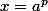
et
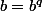
Alors comme
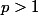
on a :
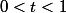
Aussi :
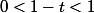
Comme la fonction ln est concave alors -ln est convexe.
Si on pose :
=-ln(x))
:
 \leq \frac{1}{p}f(a^p)+\frac{1}{q}f(b^q))
Alors :
 \leq -\frac{1}{p}ln(a^p)-\frac{1}{q}ln(b^q))
Donc en multipliant par -1 ça change le signe de l'inégalité:
 \geq \frac{1}{p}ln(a^p)\frac{1}{q}ln(b^q))
Par croissance de la fonction ln :
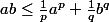
-
NicoTial
- Membre Naturel
- Messages: 81
- Enregistré le: 24 Juil 2017, 12:50
-
 par NicoTial » 11 Aoû 2017, 17:28
par NicoTial » 11 Aoû 2017, 17:28
Parfait !
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 11 Aoû 2017, 18:10
par mehdi-128 » 11 Aoû 2017, 18:10
J'ai oublié le cas a=0 ou b=0 ...
Exemple si a=0 il faut montrer :
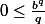
C'est évident car :
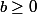
et
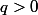
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités