Solution récurrence

[Intsugari]

Bonjour !

Je viens ici en dernier recours car je ne trouve aucune solution et je n'ai aucune idée de comment résoudre ce problème où il faut que je trouve la solution exacte de la récurrence suivante :

T(n) = 2T(n/2) + 5 ; T(1) = 1.

L'exercice qui précède est uk = 2(uk−1) + 5 ; u0 = 1.
J'ai trouvé uk = 12^n - 5 et je pense qu'il faut s'en servir mais je ne sais pas comment

[Ben314]

Salut,
Dans ta "formule" c'est quoi ? et ?
Et a priori, ça n'a rien à voir avec une récurrence qui, par essence même porte sur des nombres entiers alors que là, en général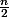 n'est pas entier.
Par exemple, tout ce que ta "formule" dit, c'est que

et, contrairement à une récurrence, ben y'a pas de raison que ça s'arrête....

[fatal_error]

@intsugari

tu peux poser n=2^k
il vient:
T(2^k) = 2T(2^{k-1})+5
puis poser u(k) = T(2^k)
u(k) = 2u(k-1)+5

[pascal16]

On peut voir ça comme une suite.
On peut la voir comme une suite arthméticogéométrique un peu bizarre, et on fait les mêmes recettes.
On calcul comme pour le point fixe l = 2l+5, soit l=-5
donc la suite V=T+5 est géométrique
soit V(n)=2 V(n/2) avec V(1)= 6

[zygomatique]

salut

si on impose à n d'être entier alors t(n) = 2t(n/2) + 5 <=> t(2n) = 2t(n) + 5

mais cette suite ne sera définie que sur une partie de N ...