Primitive

[Idefix]

Bonjour,
Quelle est la primitive de 1/ cos(x)n ?
Merci de vos réponses

[Ben314]

Salut,

Bonjour,
Quelle est la primitive de 1/ cos(x)n ?
Merci de vos réponses

HORREUR : ce n'est pas LA primitive, mais UNE (ou LES)primitive qu'on cherche.

Il y a pas mal de méthode "avec astuce" (de calcul), mais si on veut rester dans du "complétement mécanique" ne demandant aucune réflexion, on part évidement de
pour (sinon ça a pas de sens)
(1) On peut évidement utiliser le changement de variable le plus classique qui soit pour les intégrales avec fonction trigo., à savoir ce qui donne une fraction rationnelle (pourrie) dont on sait mécaniquement trouver les primitives (modulo de savoir factoriser le dénominateur, mais c'est clairement le cas ici).

(2) Un peu moins couillon : vu que la fonction est paire, si on est un peu malin on doit pouvoir poser 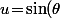dans l'intégrale çi dessus (et ça simplifie "très grandement" les calculs...)

(3) Enfin, "avec petite astuce" (mais c'est quasi la même chose que le (2)), on peut directement écrire que :

dont une primitive est claire comme de l'eau de roche...