Equation avec logarithme népérien

[Lopi987]

Bonjour j'ai une simple équation à résoudre et je bloque car je n'arrive pas à regrouper les termes



Merci pour votre aide

[zygomatique]

salut

tu ne peux pas résoudre de façon exacte cette équation !! (sauf valeur particulière ... particulière !!)

dans quel cadre t'est-il posé cette question ?

ne t'est-il pas seulement demandé qu'il existe (ou non) une solution ?

[Lopi987]

En fait pour répondre à un problème je doit résoudre le système suivant :



donc j'ai écris :

puis j'ai remplacé dans la deuxième équations.
Mais du coup je suis bien embêté
Mais en réalité on me demande une valeur approchée à de a et b mais comment faire ?

[zygomatique]

voila ce qui manquait : le dernière phrase ....

f(x) = ln(x^2) + 2/x - 1

les calculatrices donnent les solutions de l'équation f(x) = 0 ...

[Ben314]

Salut,

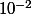
Mais en réalité on me demande une valeur approchée à de a et b mais comment faire ?

1) Il y a des logiciels qui te donne directement les solutions (approximatives) d'équation quasi quelconque, par exemple Wolfram Alpha mais :
- C'est relativement "boite noire", c'est à dire qu'on sait pas trop comment fait le programme donc c'est pas génial du tout au niveau de la compréhension du bidule.
- Beaucoup d'entre eux (pour ne pas dire tous) sont succeptible de "rater" des solutions dans certains cas très particulier.

2) Tu trace une/des courbes avec l'outil que tu préfère (calculette/géogébra/wolfram,etc...) pour déterminer graphiquement les solutions. Bien sûr tu commence par tracer la courbe sur une "grande largeur" pour voir globalement sa tête puis tu zoome sur les points qui t'intéressent pour avoir plus de précision.
Face à tu peut
- Tracer ainsi que et chercher l'intersection des deux.
- Tracer et chercher l'intersection avec l'axe des .
- Tracer et chercher l'intersection avec la droite .
- etc, etc

3) Un peu "tripatouiller" ton équation pour la ramener à quelque chose de pas trop méchant à étudier puis faire un tableau de variation pour démontrer "proprement" qu'il y a une unique solution à l'équation et avoir une idée de où se trouve cette solution.
Par exemple, ici ça semble jouable d'étudier la fonction (dérivée puis tableau de variation et éventuellement les limites) de façon à démontrer rigoureusement qu'elle ne s'annule qu'une et une seule fois.
On pourrait évidement étudier à la place la fonction pour voir combien de fois elle prend la valeur -2, sauf qu'en y regardant de plus prés, la dérivée de semble "pas très sympathique" et on risque d'avoir du mal à trouver le signe de la dérivée (à voir...)
Une fois que tu as ton tableau de variation, tu peut (par exemple par dichotomie) localiser au mieux les solutions de ton équation.
La méthode est clairement plus longue que par exemple la 2), mais à le très gros avantage de ne nécessiter qu'un outil "basique" de calcul donc qu'une telle méthode peut très facilement être implémentées dans un programme plus général de résolution d'équations (alors qu'on peut pas demander à un ordi. de directement "regarder une courbe")

Bref et en résumé, c'est pas les méthodes qui manquent et le problème, c'est plutôt de voir quelle est celle qui permet au plus vite (et avec le plus de précision) de répondre à la question.

[Lopi987]

Merci beaucoup pour tout sa je vais chercher la meilleure solution !