Devoir maison Suites

[julio567]

Bonjour je bloque sur cet exercice

Soit x un nombre réel positif ou nul et k un entier strictement supérieur à x.

A) Montrer par récurrence sur n que, pour tout entier n supérieur ou égal à k.



J'ai donc montrer par récurrence ceci est on me demande d'en déduire que pour tout entier n supérieur ou égal à k :



Comment faire ? Merci d'avance

[Pseuda]

Bonjour je bloque sur cet exercice

Soit x un nombre réel positif ou nul et k un entier strictement supérieur à x.

A) Montrer par récurrence sur n que, pour tout entier n supérieur ou égal à k.



J'ai donc montrer par récurrence ceci est on me demande d'en déduire que pour tout entier n supérieur ou égal à k :



Comment faire ? Merci d'avance

Bonjour,

[julio567]

Bonjour je bloque sur cet exercice

Soit x un nombre réel positif ou nul et k un entier strictement supérieur à x.

A) Montrer par récurrence sur n que, pour tout entier n supérieur ou égal à k.



J'ai donc montrer par récurrence ceci est on me demande d'en déduire que pour tout entier n supérieur ou égal à k :



Comment faire ? Merci d'avance

Bonjour,

Tout d'abord merci de votre réponse. Ah c'est simplement ce qu'il fallait faire ?

[Pseuda]

Oui c'est tout. ?? En ayant bien sûr supposé au préalable que , et en utilisant le résultat de la récurrence.

[julio567]

Oui c'est tout. ?? En ayant bien sûr supposé au préalable que , et en utilisant le résultat de la récurrence.

Merci beaucoup pseuda et une dernière chose si vous pouviez me venir en aide on me demande de montrer que la limite quand n temps vers plus l'infini de

x^n est toujours positif
n! va être positif vu que n est superieur ou egal a k et que k est strictement supérieur a x (or x est positif) je ne vois donc pas comment elle pourrais tendre vers 0 pouviez vous m'expliquez ?

[Pseuda]

Oui c'est tout. ?? En ayant bien sûr supposé au préalable que , et en utilisant le résultat de la récurrence.

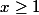
J'ai répondu un peu vite. Il faut distinguer le cas et , mais dans les deux cas ...

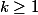
[Pseuda]

Merci beaucoup pseuda et une dernière chose si vous pouviez me venir en aide on me demande de montrer que la limite quand n temps vers plus l'infini de

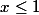
Ceci est faux pour ? Et même pour tout ?

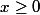
Je suppose que tu dois démontrer que la limite est 0. Ce n'est pas une question d'être positif ou non, tous les termes de l'inégalité sont positifs. Il faut utiliser l'inégalité trouvée et le théorème de comparaison.

Indice : et k est arbitraire.