Polynome de second degré

[jsp]

Bonjour je voudrais savoir si le a de la formule ax^2+bx+c est l'ordonnée à l'origine ?
Merci

[Pseuda]

Bonjour,

Pas du tout. Dans le cas d'une fonction quelconque, ce qu'on pourrait appeler l'ordonnée à l'origine serait l'image de la fonction en 0, c'est-à-dire f(0), soit pour ce polynôme : f(0)=c.

On utilise cette expression plutôt dans le cas d'une fonction affine : f(x) = ax +b ; b est l'ordonnée à l'origine.

[Dasson2]

Bonjour,
l'ordonnée à l'origine est l'ordonnée pour x= 0 donc ici c'est c.
Plus utilisée pour une droite y=ax+b : l'ordonnée à l'origine est alors b, c'est l'ordonnée du point d'intersection de la droite avec l'axe des ordonnées.
Message croisé...

[jsp]

Merci, c 'est parce que je cherche comment trouver la valeur a grâce à l'aide de la représentation graphique et des valeurs alpha et beta et je n'y arrive pas

[Pseuda]

Tu veux parler de la forme canonique : ?

Pour trouver a graphiquement, tu peux déterminer sur ton graphique, tu obtiens : . Tu n'as plus qu'à diviser par .

[Dasson2]

Il peut être utile de savoir que le sommet de la parabole a pour coordonnées x=-b/2a et y= (4ac-b²)/4a

[jsp]

Donc ça voudrait dire que a est le resultat de alpha divisé par beta ? Parce que sur ma courbe je ne lis que la valeur de alpha et beta ( qui sont en autre le minimum de ma courbe avec alpha abscisse et beta ordonnée )

[Pseuda]

Peux-tu montrer ta courbe ?

Parce que si le sommet de ta courbe se situe en , c'est que a = 1.

[Ben314]

Salut,
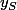Je ne pense pas que ce soit ce qui est attendu, mais si ça t'amuse, tu peut montrer que, lorsqu'une parabole a pour équation y=ax²+bx+c, une méthode graphique pour "lire" le coefficient a, c'est d'utiliser le fait que où et 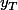sont les ordonnées respectives du sommet de la parabole (où la tangente est horizontale) et du point de la parabole où la tangente à une pente égale à 1 (i.e. est parallèle à la première bissectrice d'équation y=x).