Besoin d'aide

[Amélia]

Bonsoir à tous! Quelqu'un pourrait me guider pour la 2e expression de la 3e question ? A la première expression je trouve 2^n, mais à la deuxième, j'ai toujours des toujours des sigmas dans mes expressions et n'arrive pas à m'en débarrasser...

[Ben314]

Salut,
Je te fait le principe pour le deuxième pour que tu voie la logique du chmilblick :




Car , donc et

Donc

[Razes]

Écris tes expressions et identifie les formes suivantes:

[Amélia]

j^3k + j^3k+1 + j^3k+2?

[Amélia]

Razes : (1+j)^(3k+1) + (1+j²)^(3k/2+1/2) + (1+j³)^(k) ?

[Razes]

Razes : (1+j)^(3k+1) + (1+j²)^(3k/2+1/2) + (1+j³)^(k) ?

, applique la formule du binôme.

[Amélia]

Je trouve :
(1+j)^n = 1*(j^3k+1)
(1+j²)^n = 1*(j^6k+4)
(1+j³)^n = (1+1)^n = 1*1^3k = 1

[Razes]

Razes : (1+j)^(3k+1) + (1+j²)^(3k/2+1/2) + (1+j³)^(k) ?

, applique la formule du binôme.

[samoufar]

Bonsoir,

On peut s'affranchir de la formule du binôme en remarquant que (somme des racines cubiques de l'unité). Ça a normalement été vérifié à la question 1.

[Razes]

Bonsoir,

On peut s'affranchir de la formule du binôme en remarquant que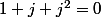 (somme des racines cubiques de l'unité). Ça a normalement été vérifié à la question 1.

Oui, mais dans un premier temps, l'objectif est que Amélia puisse faire le rapprochement entre cette expression et ce qu'a développé Ben314. Après, effectivement elle utilise l'expression déjà trouvée pour terminer le calcul.

[Amélia]

J'applique bien la formule du binome (1+j)^n = sigma( 3k+1 parmi n ) 1*j^(3k+1)
(1+j²)^n = sigma(3k+2 parmi n) 1*(j^6k+4)
(1+j³)^n = (1+1)^n = sigma (3k parmi n ) 1*1^3k = 1 et je ne peux pas simplifier en sommant les trois termes .. Je ne vois pas, je dois mal comprendre... J'avais remarqué l'addition des coefficients 1 + j + j² mais le problème est que je n'arrive pas à avoir trois fois la même somme pour pouvoir simplifier

[Ben314]

Sauf que quand je vois ça :

(1+j)^n = 1*(j^3k+1)
(1+j²)^n = 1*(j^6k+4)

ben déjà je me dit que c'est pas gagné....

Amélia, pour toi, le qu'il y a à droite dans ton expression, il représente quoi ?
Plus précisément, lorsque par exemple je prend n=5, tu est bien d'accord que (1+j²)^5, ça représente un et un unique nombre complexe qui ne dépend... de rien du tout...
Et dans ce cas, ton , il vaut combien ? et pourquoi ?

Ensuite, quand je vois ça :

(1+j³)^n = (1+1)^n = 1*1^3k = 1

alors là, c'est :
Non seulement je comprend pas comment peut débarquer un "k" dans une expression qui au départ dépend de "n", mais en plus de voir écrit noir sur blanc que, par exemple (1+1)^3, c'est à dire 2x2x2 ça fait 1, là,....

[Amélia]

Oui effectivement je sais que je comprends pas comment bien utiliser la formule, mais quand j'écris 1*1^3k c'est plutôt à 1*(1^3k) que je pense... Pour moi sinon, (1+j)^n = sigma( 3k+1 parmi n ) (1^n-(3k+1))*j^(3k+1) ... Merci d'avoir pris du temps pour essayer de m'expliquer

[samoufar]

Pour moi sinon, (1+j)^n = sigma( 3k+1 parmi n ) (1^n-(3k+1))*j^(3k+1) ...

Je ne vois pas comment tu obtiens cette formule, parce qu'en simplifiant tes termes, le 1^... vaut 1 et le j^(3k+1) vaut j...

Par contre tu as par la formule du binôme de Newton

et d'un autre côté