Demonstration
27 messages
- Page 1 sur 2 - 1, 2
Re: demonstration
bonjour
bonjour et merci ? un autre jour peut-etre!
j'imagine que l'equation est
sin³(x) + cos³(x) = 1
dans ce cas sin³(x) + cos³(x) = 1 = cos²(x) + sin²(x)
en mettant en facteurs ....
bonjour et merci ? un autre jour peut-etre!
j'imagine que l'equation est
sin³(x) + cos³(x) = 1
dans ce cas sin³(x) + cos³(x) = 1 = cos²(x) + sin²(x)
en mettant en facteurs ....
Re: demonstration
siger pardonnez moi vraiment .
je me bloque dans cette etape sin³(x) + cos³(x)= cos²(x) + sin²(x)
Merci d'avance
je me bloque dans cette etape sin³(x) + cos³(x)= cos²(x) + sin²(x)
Merci d'avance
Re: demonstration
Re
si tu mettais en facteur cos²(x) et sin²(x)
on obtient cos²(x) (cos(x) -1)+ sin²(x) (sin(x)-1)
qui s'annule ...........
si tu mettais en facteur cos²(x) et sin²(x)
on obtient cos²(x) (cos(x) -1)+ sin²(x) (sin(x)-1)
qui s'annule ...........
Re: demonstration
re
avant de continuer j'aimerais que tu confirmes l'enoncé.......
cos³(x) + sin³(x) = 1
Montrer que (cosx=1 et sinx=0) ou (sinx=1 et cosx=0)
la reponse me parait triviale s'il ne s'agit que de "montrer"
.
par contre l'enoncé
cos(3x) + sin(3x) = 1 est un peu moins simple.......
avant de continuer j'aimerais que tu confirmes l'enoncé.......
cos³(x) + sin³(x) = 1
Montrer que (cosx=1 et sinx=0) ou (sinx=1 et cosx=0)
la reponse me parait triviale s'il ne s'agit que de "montrer"
.
par contre l'enoncé
cos(3x) + sin(3x) = 1 est un peu moins simple.......
Re: demonstration
L'ennoncé c'est : soit x appartenant a IR tel que : cos³(x) + sin³(x) = 1
Montrer que (cosx=1 et sinx=0) ou (cosx=0 et sin x= 1)
Et merci encore
Montrer que (cosx=1 et sinx=0) ou (cosx=0 et sin x= 1)
Et merci encore
Re: demonstration
Les seules solutions possibles sont :
ou
Remarque: L'expression
CQFD
Re: demonstration
salut
on y arrive aussi en posant t=tan(x/2)
il faut résoudre
2t²(t-1)²(t²+2t+3)=0
facile
on y arrive aussi en posant t=tan(x/2)
il faut résoudre
2t²(t-1)²(t²+2t+3)=0
facile
Re: demonstration
Bonsoir,
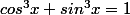 si et seulement si
si et seulement si 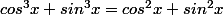
soit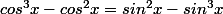
soit = sin^2x (1 - sin x ))
Que peux-tu dire du signe de l'expression de droite, et du signe de celle de gauche ?
A quelle condition ces 2 expressions sont égales ?
soit
soit
Que peux-tu dire du signe de l'expression de droite, et du signe de celle de gauche ?
A quelle condition ces 2 expressions sont égales ?
Re: demonstration
Ok. Signe de 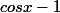 ? Donc signe de
? Donc signe de  ?)
Signe de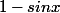 ? donc signe de
? donc signe de ) ?
?
Conclusion : ces 2 expressions ne peuvent être égales que si elles sont toutes les 2 nulles. Je te laisse terminer....
Signe de
Conclusion : ces 2 expressions ne peuvent être égales que si elles sont toutes les 2 nulles. Je te laisse terminer....

Re: demonstration
Peut tu me dire les etapes qu'on a fait pour constaté qu'elles sont nulles svp ne me pose pas des questions si c'est possible et merci infiniment
Re: demonstration
par Razes » 11 Sep 2016 22:58
par Pseuda » 12 Sep 2016 19:30
@Pseuda
Bonsoir, Il y a quoi de neuf dans ta résolution par rapport à la mienne?
Razes a écrit:(1)
(2)
(\cos (x)-1)+\sin^2(x)(\sin (x)-1)=0\Leftrightarrow (1-\sin^2(x))(\cos (x)-1)+(1-\cos^2(x))(\sin (x)-1)=0\Leftrightarrow)
Les seules solutions possibles sont :; donc d'après (2);
ou; donc d'après (2);
Remarque: L'expressionn'est jamais nulle, facile à démontrer
CQFD
par Pseuda » 12 Sep 2016 19:30
Pseuda a écrit:Bonsoir,si et seulement si
soit
soit
Que peux-tu dire du signe de l'expression de droite, et du signe de celle de gauche ?
A quelle condition ces 2 expressions sont égales ?
@Pseuda
Bonsoir, Il y a quoi de neuf dans ta résolution par rapport à la mienne?
Re: demonstration
Bonjour,
@Razes,
Mais elle n'a rien à voir, tu ne t'en rends pas compte ?
Non sérieusement, je trouve que ta démonstration est assez compliquée, car elle fait appel à une factorisation qui n'est pas simple pour le lycée, technique pas toujours bien maîtrisée à ce stade.
@Razes,
Mais elle n'a rien à voir, tu ne t'en rends pas compte ?
Non sérieusement, je trouve que ta démonstration est assez compliquée, car elle fait appel à une factorisation qui n'est pas simple pour le lycée, technique pas toujours bien maîtrisée à ce stade.
Re: demonstration
anassmsdq a écrit:Peut tu me dire les etapes qu'on a fait pour constaté qu'elles sont nulles svp ne me pose pas des questions si c'est possible et merci infiniment
Bonjour,
En quelle classe es-tu ?
Tu dois savoir depuis la 2nde que :
Et que :
27 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
