Taux d'accroissement; dérivée en 1 point

[PatoOo]

Bonjour à tous,

me revoici avec un nouvel exercice sur les taux d'accroissement et le nombre dérivé aux points donnés

voici sur quoi je bloque
en

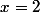
j'ai donc fait comme ceci :

est-ce que jusque là, c'est bon ?

qu'est ce que je dois faire ensuite, la dérivée de ce truc ??

merci !

[Ben314]

Salut,
Non, ce n'est pas bon du tout de chez pas bon du tout.
- Déjà, avant même d'écrire b'(2)=quelque chose, il faudrait avoir montré que b'(2) existe.
- Ensuite, modulo qu'il existe, il n'est absolument pas égal à ce que tu écrit vu que ce que tu écrit dépend d'une variable h alors qu'évidement, b'(2) ne dépend de rien du tout.
- Enfin, il faudrait peut être réviser les cours de collège où on a du te signaler de multiples fois que racine(A+B) n'est pas du tout égal à racine(A)+racine(B).

[PatoOo]

Salut,
Non, ce n'est pas bon du tout de chez pas bon du tout.
- Déjà, avant même d'écrire b'(2)=quelque chose, il faudrait avoir montré que b'(2) existe.
- Ensuite, modulo qu'il existe, il n'est absolument pas égal à ce que tu écrit vu que ce que tu écrit dépend d'une variable h alors qu'évidement, b'(2) ne dépend de rien du tout.
- Enfin, il faudrait peut être réviser les cours de collège où on a du te signaler de multiples fois que racine(A+B) n'est pas du tout égal à racine(A)+racine(B).

ok

alors je reprends
1) comment je fais pour démontrer que b'(2) existe ?

2 ) il faut bien que j'utilise cette formule ?

sinon, je veux bien que tu m'expliques comment procéder stp

[Manny06]

pour une expression de la forme
(Vu(h)-V11)/h multiplie haut et bas par l'expression conjuguée Vu(h)+V11
ensuite simplifie par h puis cherche la limite quand h tend vers 0