Bonjour à tous.
Voilà j'ai un exercice à faire, mais je bloque totalement!! C'est pourquoi j'ai besoin d'aide.
Soit f la fonction définie sur R par f(x)=(e^x-3)/(e^x+1) et C sa courbe représentative dans un repère du plan.
Justifier les quatre affirmations suivantes:
A1/ Pour tout x réel on peut écrire: f(x)=-3+(4e^x/e^x+1)
f(x)=(1-3e^-x)/(1+e^-x)
A2/ La tangente à la courbe C au point B d'abscisse nulle a pour équation y=x-1
A3/ La courbe C coupe l'axe des abscisses en un point unique dont l'abscisse 'a' vérifie 1<A<1.1
A4/ Pour tout x réel -3<f(x)<1
Merci d'avance pour votre aide.
Fonction exponentielle
4 messages
- Page 1 sur 1
Re: Fonction exponentielle
Bonjour,
A1 le numérateur de f(x) peut s'écrire
pour la 2ème relation factorise le numérateur et le dénominateur par
A2 rappel: l'équation de la tangente au point d'abscisse a s'écrit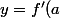(x-a)+f(a))
A1 le numérateur de f(x) peut s'écrire
pour la 2ème relation factorise le numérateur et le dénominateur par
A2 rappel: l'équation de la tangente au point d'abscisse a s'écrit
Re: Fonction exponentielle
Merci pour votre aide.
Par contre pour la A3 je bloque.
A3/ La courbe C coupe l'axe des abscisses en un point unique dont l'abscisse 'a' vérifie 1<a<1.1
Faut faire: f(x)=0 donc : (e^x-3)/(e^x+1)=0 ???
Par contre pour la A3 je bloque.
A3/ La courbe C coupe l'axe des abscisses en un point unique dont l'abscisse 'a' vérifie 1<a<1.1
Faut faire: f(x)=0 donc : (e^x-3)/(e^x+1)=0 ???
Re: Fonction exponentielle
oui
f(x)=(e^x-3)/(e^x+1) =0
donc annule le numérateur
e^x-3=0
x=Ln(3)=1,09...
f(x)=(e^x-3)/(e^x+1) =0
donc annule le numérateur
e^x-3=0
x=Ln(3)=1,09...
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
