Correction incompréhensible

[lucieemtl]

Bonsoir à tous et à toutes.

Voilà il y'a une correction d'une inéquation que je ne comprends pas très bien.

L'expression est 2ln(x)+1>0 sur ]0;+[
Et la correction donne x>1/Racine carrée d'exponentielle
Je ne comprends pas pourquoi

[aymanemaysae]

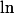
Premièrement donnez une expression où on a le d'un côté du signe > et un nombre de l'autre, après on verra.

[lucieemtl]

J'ai très bien compris qu'il fallait procéder ainsi, soit dans un premier temps faire :
2ln(x)>-1
Puis ln(x)>-1/2

Mais après.. Je suis largué....

[aymanemaysae]

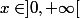
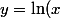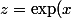La fonction exponentielle est la fonction réciproque de la fonction logarithme, c-à-d que si et si on a alors on a , et si x on a alors .

En général, si g est la fonction réciproque de la fonction f alors on a f(g(x)) = x ou g(f(x)) = x dans les domaines de validité de ces opérations .

Donc pour votre exemple , on a : , donc comme la fonction exponentielle est strictement croissante sur alors elle garde le sens de l'inégalité donc ..........