Bonsoir à tous et à toutes,
Je prépare l'examen du BTS SIO (Services Informatiques aux Organisations) cette année, et dans mes révisions je me consacre aux mathématiques pour le moment.
Toutefois, j'ai un peu de mal avec les logarithmes et exponentielles et j'aimerai savoir si quelqu'un a une méthode toute simple pour résoudre tout type d('in)équation avec logarithmes et exponentielles ?
Cordialement,
Bonne soirée.
Lucie MUTEREL
Méthode pour résoudre une (in)équation avec logarithme
12 messages
- Page 1 sur 1
Re: Méthode pour résoudre une (in)équation avec logarithme
Bonsoir,
Je pense qu'il n'y a pas de méthode générale pour résoudre ces exercices.
Donne nous un exemple afin de préciser un peu mieux ta demande.
Je pense qu'il n'y a pas de méthode générale pour résoudre ces exercices.
Donne nous un exemple afin de préciser un peu mieux ta demande.
Re: Méthode pour résoudre une (in)équation avec logarithme
C'est en forgeant qu'on devient forgeron, et en faisant beaucoup d'exercices vous arriverez à résoudre 80% des exercices qui se présenteront: les 20% restant sont pour les génies.
D'autre part, il n' y a pas de méthode pour résoudre automatiquement un exercice avec des logarithmes et des exponentielles: on traite les exercices cas par cas, ou c'est tout au moins ce que pense.
Pour rester positif, voici un exercice avec sa solution pour étayer ce que j'ai dit:
Résoudre - \ln(x) - 2 = 0 \rightarrow \ln^2(x) - 2 \frac{1}{2}\ln(x) + \frac{1}{4} - \frac{1}{4} - 2 = 0 \rightarrow \ln^2(x) - 2 \frac{1}{2}\ln(x) + \frac{1}{4} - \frac{9}{4} = 0 \rightarrow (\ln(x) - \frac{1}{2})^2 - (\frac{3}{2})^2 = 0)
 - \frac{1}{2} - \frac{3}{2}) - (\ln(x) - \frac{1}{2} + \frac{3}{2})= 0 \rightarrow (\ln(x) - 1) - (\ln(x) + 1)= 0 \rightarrow \ln(x) 2 ou \ln(x) = - 1 \rightarrow x = \exp(2) ou x = \exp(- 1) = \frac{1}{e}.)
Bon courage.
D'autre part, il n' y a pas de méthode pour résoudre automatiquement un exercice avec des logarithmes et des exponentielles: on traite les exercices cas par cas, ou c'est tout au moins ce que pense.
Pour rester positif, voici un exercice avec sa solution pour étayer ce que j'ai dit:
Résoudre
Bon courage.
Re: Méthode pour résoudre une (in)équation avec logarithme
Là comme ça comment résoudriez-vous cet équation 3ln(x+1)-3=0 par exemple ?
Re: Méthode pour résoudre une (in)équation avec logarithme
aymanemaysae je ne comprends pas d'où proviennent les 1/4 

Re: Méthode pour résoudre une (in)équation avec logarithme
Perso, comme exemple d'exercice "de base", j'aurais plutôt vu un truc du style :
-\ln(x+1)=1+\ln(x))
Qu'un où on vire immédiatement le logarithme en posant X=ln(x)...
Qu'un où on vire immédiatement le logarithme en posant X=ln(x)...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Méthode pour résoudre une (in)équation avec logarithme
lucieemtl a écrit:Là comme ça comment résoudriez-vous cet équation 3ln(x+1)-3=0 par exemple ?
Ce type d'exo, c'est fastoche :
a) Tu commence par simplifier si tu peut (ici, tu peut...)
b) Tu écrit ton truc sous la forme ln(????)=constante
c) Tu dit que c'est équivalent à ????=exp(constante) et là, tu as plus de logarithme.
Et on peut dire que cette "méthode" s'applique à pas mal d'équations (pas toutes évidement) vu qu'à l'aide de la propriété caractéristique du log, à savoir ln(ab)=ln(a)+ln(b), il y a un certain nombre d'équation qui se ramènent à ln(????)=cst.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Méthode pour résoudre une (in)équation avec logarithme
Pensez toujours que vous pouvez tôt ou tard vous débarrasser des 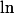 ou des
ou des 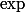 .
.
 - 3 = 0 \rightarrow 3 \ln(x+1) = 3 \rightarrow \ln(x+1) = 1 \rightarrow \exp(\ln(x+1)) = \exp(1) \rightarrow x + 1= e\rightarrow x = e - 1.)
Dites-moi maintenant quelle étape de la résolution de cet exercice qui vous pose un problème?
Dites-moi maintenant quelle étape de la résolution de cet exercice qui vous pose un problème?
Re: Méthode pour résoudre une (in)équation avec logarithme
@aymanemaysae : est-ce que, a force, tu va finir par te décider à appliquer la charte du Forum ou bien c'est vraiment désespéré ?
jb13 a écrit:Note aux correcteurs :
Au cas par cas, lorsqu'il est avéré que l'élève est vraiment perdu dans la résolution d'un problème, qu'il respecte tous les points de la charte (politesse, etc.) et qu'il est de bonne foi (effort de recherche, volonté d'essayer, etc.), il est possible que le correcteur donne une réponse complète. Il est toutefois interdit de le faire si un autre intervenant est en cours d'échange avec l'élève. Dans tous les autres cas, il est demandé au correcteur de guider progressivement l'élève vers la résolution complète de son énoncé.
Lorsqu'un correcteur donne ipso facto la réponse complète à un élève sans que celui-ci n'ait fourni un effort de recherche ou ne paraisse complètement perdu, il est convenu que le modérateur le prévienne par message privé de son comportement contraire à la charte.
Surtout qu'il faudrait savoir ce que tu pense : les exos, il faut qu'il les cherche ou qu'il lise tes corrections ?aymanemaysae a écrit:C'est en forgeant qu'on devient forgeron, et en faisant beaucoup d'exercices vous arriverez à résoudre 80% des exercices qui se présenteront: les 20% restant sont pour les génies.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Méthode pour résoudre une (in)équation avec logarithme
Non, je ne voulais pas enfreindre la charte, mais je croyais avoir deviné ou notre ami avait un problème: la composition des fonctions exponentielle et logarithme pour faire apparaître les 'x' .
Je demande quand même pardon, mais le zèle de la jeunesse l'emporte quelques fois sur ce que la sérénité nous conseille.
Je demande quand même pardon, mais le zèle de la jeunesse l'emporte quelques fois sur ce que la sérénité nous conseille.
Re: Méthode pour résoudre une (in)équation avec logarithme
salut
perso lorsque je fais mon cours sur ln et exp je commence par le basique de chez basique ....
f désigne ln ou exp, g désigne la réciproque de f
T désigne < ou > ou =< ou >=
a et r désignent deux réels "adéquats" et x est la variable bien sur ...
alors deux cas :
f(x) = f(a) <=> x = a (justifier pourquoi on se "débarrasse" de f)
f(x) T f(a) <=> x T a (idem)
ou
f(x) = r <=> x= g(r) (idem)
f(x) T r <=> x T g(r) (idem)
quand on a bien compris cela alors il est aisé de complexifier l'(in)équation ....

j'ai bien sur formaliser ici pour condenser les deux cours ....
perso lorsque je fais mon cours sur ln et exp je commence par le basique de chez basique ....
f désigne ln ou exp, g désigne la réciproque de f
T désigne < ou > ou =< ou >=
a et r désignent deux réels "adéquats" et x est la variable bien sur ...
alors deux cas :
f(x) = f(a) <=> x = a (justifier pourquoi on se "débarrasse" de f)
f(x) T f(a) <=> x T a (idem)
ou
f(x) = r <=> x= g(r) (idem)
f(x) T r <=> x T g(r) (idem)
quand on a bien compris cela alors il est aisé de complexifier l'(in)équation ....
j'ai bien sur formaliser ici pour condenser les deux cours ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
