Méthode pour equation avec racines carrés
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Azuriel
- Membre Relatif
- Messages: 236
- Enregistré le: 28 Déc 2006, 16:48
-
 par Azuriel » 28 Déc 2006, 16:52
par Azuriel » 28 Déc 2006, 16:52
Bonjour je voulais savoir si vous pouviez me donner une méthode afin de résoudre cette equation :
J'utiliserai V pour racine
V(x-9) + V(x-24) = x
Merci d'avance :happy2:
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 28 Déc 2006, 17:05
par fahr451 » 28 Déc 2006, 17:05
V(x-9) < x/2 (élever au carré discrimant négatif) idem pour l 'autre donc pas de solution
-
Azuriel
- Membre Relatif
- Messages: 236
- Enregistré le: 28 Déc 2006, 16:48
-
 par Azuriel » 28 Déc 2006, 17:08
par Azuriel » 28 Déc 2006, 17:08
pourquoi tu majore par x/2 ?? J'ai pas tres bien compris la methode..
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 28 Déc 2006, 17:15
par fahr451 » 28 Déc 2006, 17:15
parce que cela permet de conclure
es tu d'accord avec la majoration?
-
Azuriel
- Membre Relatif
- Messages: 236
- Enregistré le: 28 Déc 2006, 16:48
-
 par Azuriel » 28 Déc 2006, 17:21
par Azuriel » 28 Déc 2006, 17:21
En fait je ne vois pas où comment tu l'as trouver..
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 28 Déc 2006, 17:23
par fahr451 » 28 Déc 2006, 17:23
sortie du chapeau
en fait comme x>24; racine de x est vraiment petit par rapport à x donc l'équation a peu de "chance" d'avoir de solution (justification empirique)
-
Azuriel
- Membre Relatif
- Messages: 236
- Enregistré le: 28 Déc 2006, 16:48
-
 par Azuriel » 28 Déc 2006, 17:28
par Azuriel » 28 Déc 2006, 17:28
et sinon pour des equation de ce genre avec des solutions, quelle serait la méthode ?
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 28 Déc 2006, 17:38
par fahr451 » 28 Déc 2006, 17:38
et sinon ...
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 28 Déc 2006, 19:18
par BancH » 28 Déc 2006, 19:18
Azuriel a écrit:et sinon pour des equation de ce genre avec des solutions, quelle serait la méthode ?
Comme

?
-
Azuriel
- Membre Relatif
- Messages: 236
- Enregistré le: 28 Déc 2006, 16:48
-
 par Azuriel » 28 Déc 2006, 19:23
par Azuriel » 28 Déc 2006, 19:23
Oui par exemple, enfin quand il ya un x de l'autre coté car apres en manipulant les carré ça nous fait des equation du 4eme degré alors...
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 28 Déc 2006, 20:55
par yos » 28 Déc 2006, 20:55
On élève au carré : reste une racine qu'on isole. On recommence.
Prudence : l'élévation des deux membres au carré agrandit l'ensemble de solution.
-
mathelot
 par mathelot » 28 Déc 2006, 23:21
par mathelot » 28 Déc 2006, 23:21
l'introduction de la quantité conjuguée permet de descendre le degré de l'équation de 1. L'équation de Banch n'a pas de solution.
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 28 Déc 2006, 23:43
par BancH » 28 Déc 2006, 23:43
Bah si, je l'ai prise exprès, la solution c'est vingt-cinq.
-
mathelot
 par mathelot » 29 Déc 2006, 18:59
par mathelot » 29 Déc 2006, 18:59
résoudre et discuter:

ou alors celle-là:

-
mathelot
 par mathelot » 30 Déc 2006, 12:44
par mathelot » 30 Déc 2006, 12:44
elles plaisent à personne mes équations ? indication: utiliser la quantité conjuguée.
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 02 Jan 2007, 18:56
par BancH » 02 Jan 2007, 18:56
Pour la deuxième, je trouve
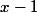
solutions:
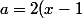-(x-1)^2)
et

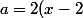-(x-2)^2)
et

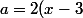-(x-3)^2)
et

...

et
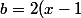-(x-1)^2)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
