Rayon de convregence

[smmo1986]

bonjour tout le monde
j ai deux séries entiere : Σ(z^n/n) et Σ(z^n/n^2)

pourquoi celle là Σ(z^n/n^2) on R=1 et pour la déxieme on trouve R=1 MAIS ON ETUDIE le cas ou z=1 ? pourquoi ?

[Ben314]

Salut,
La seule réponse qui me vient à l'esprit, c'est "parce qu'on te demande de la faire..."
De façon très générale, tu doit évidement savoir que, si R désigne le rayon de c.v. d'une série entière, alors la série est c.v. pour tout z tel que |z|<R et qu'elle est divergente pour |z|>R (c'est le B-A-BA).
Après, dans le cas où |z|=R, l'éventuelle convergence va dépendre de la série ET du z choisi.

Dans certains cas (comme pour les deux d'ici), on arrive à répondre à la question "quels sont les z de module R tels que la série soit convergente ?" (question qu'on ne se pose pas systématiquement).
Sauf que la valeur z=1 (qui est bien de module 1=R) ne joue pas franchement un rôle particulier dans le cas de la deuxième série : on montre facilement que tout z de module R(=1) donne le même type de comportement.

Sinon, concernant la première série, c'est un peu différent, le cas z=1 (de module R=1) est facile à traiter, mais le cas des autres z de module R(=1) est plus technique...

P.S. Ou alors j'ai mal compris ta question et ce que vous avez fait pour la deuxième série, c'est de commencer par regarder la convergence en z=1 pour ensuite en déduire le rayon de C.V. de la série.

[alm]

Bonjour

pour la déxieme on trouve R=1 MAIS ON ETUDIE le cas ou z=1 ? pourquoi ?

Tu veux dire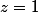 ou ?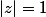
On profite peut être de l'occasion de la convergence de la série de Riemann pour en déduire qu'il y a en fait convergence absolue de la série entière en question sur son disque fermée de convergence. En pourquoi pas puisque c'est facile à faire.