Exercice Trigo Terminale S

[fly737]

Bonjour,

J'ai besoin de votre aide svp pour cet exercice !

On désigne par f la fonction numérique définie par:
f(x)= 2x- Sin x
et on appelle C sa courbe représentative dans un repère orthonormé (O;i;j). L'objet de cet exercice est une étude précise de la fonction f et de sa courbe représentative C.

1) Calculer la dérivée de f et en déduire le sens de variation de f sur R. Montrer que pour tout x de R : 2x-1 ;) f(x) ;) 2x+1
Pour cet question pas de problème je pars du principe que -1 ;) -Sin x ;) 1
En déduire les limites de f lorsque x tend vers + ;) et vers - ;)
J'ai trouvé lim f(x)= +;) lorsque x tend vers + ;) (théorème des gendarmes)
et lim f(x)=- ;) lorsque x tend vers - ;)

2) On appelle D1 et D2 les droites d'équations respectives :
y = 2x -1 et y = 2x + 1

Déterminer les points communs a C et D1 d'une part, à C et D2 d'autre part. Préciser les tangentes à C en ces points.
Pour cette question j'ai trouvé:
Sin x = -1 (pour x=-;)/2 +2k;))
Et Sin x=1 (pour x=;)/2 +2k;))
Après je sais pas répondre à la question:"Préciser les tangentes à C en ces points"

3) Etudier la parité de la fonction f.

Calculer f(x+2;)) en fonction de f(x).
Pas de difficulté, j'obtiens: f(x+2;))=f(x)+4;)

Par quelle transformation géométrique passe t-on de la partie de C représentant la restriction de f à [-;);;)] à la partie de C représentant la restriction de f à R- ?
Je bloque sur cette question

Par quelle transformation géométrique passe t-on de la partie C représentant la restriction de f à R+ à la partie de C représentant la restriction de f à [-;) + 2k;); ;) + 2k;)] ? (k appartient a Z)
Je bloque de même sur cette question

4) Tracer avec précision sur papier millimétré dans le repère (O,i,j) (unité 2cm) la courbe C sur l'intervalle [0, ;)].

Déterminer et tracer les tangentes au point O et au point A d'abscisse ;), tracer également D1 et D2.
Pour tracer, pas de problème mais pour déterminer, je ne vois pas ce qu'il faut dire

Je vous remercie d'avance !

[Ben314]

Salut,
Tes réponses aux questions 1) et 2) sont correctes et à la fin de la question 2, ben on te damande de déterminer l'équation de la tangente à la courbe en un point d’abscisse , 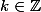ainsi qu'en un point d'abscisse , .
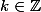Si tu as un peu de bon sens géométrique, les résultat sont complètement évidents, mais a mon avis, on te demande de faire le calcul pour vérifier.

3) Le fait que signifie que, si le point est sur la courbe (c'est à dire si ) alors le point est aussi sur la courbe (car ).
Comment "passe t-on" géométriquement de M à N ?

4) On te demande de trouver par le calcul l'équation de la tangente à la courbe au point O (d’abscisse ) ainsi que celle au point A (d'abscisse ).
Tu ne sait pas quelle est l'équation de la tangente à la courbe d'une fonction f au point d'abscisse ?

[fly737]

Salut,
Merci pour ta réponse j'ai mis pour la question 1:
La tangente en pi/2 correspond à y=2x+1 et la tangente en -pi/2 x est 2x-1
Par contre je ne vois pas quel calcul dois-je effectuer

[fly737]

Euh non l'inverse pour -pi/2 c'est y=2x+1 et pour pi/2 y=2x-1

[fly737]

Et pour la question on passe de M à N par translation ?