Bonjour j'ai cet exercice à faire et je voudrai savoir comment montrer la question 2 et la question 3.
Je vous remercie d'avance.
Soit f lapplication de lintervalle ]0, 1] dans R dé;)nie par:
.f(1/n)= 1/(n+1)pour tout entier naturel non nul n,
.f (x) = x si x nest pas linverse dun entier naturel.
A;)n déviter toute confusion, on utilise ici la notation anglo-saxonne pour lécriture des nombres
décimaux , avec un point "." plutôt quune virgule "," pour séparer parties entière et décimale.
1. Déterminer f (0.1), f (0.2), f (0.3) et f (0.5).
A;)n déviter toute confusion, on utilise ici la notation anglo-saxonne pour lécriture des nombres
décimaux , avec un point "." plutôt quune virgule "," pour séparer parties entière et décimale.
2. Montrer que f est injective.
3. Montrer que f]0,1]=]0,1[
.
Application (exo pour demain)
4 messages
- Page 1 sur 1
Pour la question 2, et pour simplifier l'écriture, vous pouvez poser : A={ tel que n
tel que n  IN*},
IN*},
et étudier l'injectivité par séparation des cas:
1) u A et v
A et v  A
A
2) u ]0,1]\A et v
]0,1]\A et v  ]0,1]\A
]0,1]\A
3) Pour le cas u A et v
A et v  ]0,1]\A et vice versa , écrire f(u) = f(v) est impossible
]0,1]\A et vice versa , écrire f(u) = f(v) est impossible
car pour le cas u A et v
A et v  ]0,1]\A , il existe s
]0,1]\A , il existe s IN* tel que u =
IN* tel que u =
et donc f(u) = f(v)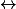 f(
f( ) = v
) = v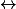
 = v : contradiction .
= v : contradiction .
et étudier l'injectivité par séparation des cas:
1) u
2) u
3) Pour le cas u
car pour le cas u
et donc f(u) = f(v)
aymanemaysae a écrit:Pour la question 2, et pour simplifier l'écriture, vous pouvez poser : A={tel que n
IN*},
et étudier l'injectivité par séparation des cas:
1) uA et v
A
2) u]0,1]\A et v
]0,1]\A
3) Pour le cas uA et v
]0,1]\A et vice versa , écrire f(u) = f(v) est impossible
car pour le cas uA et v
]0,1]\A , il existe s
IN* tel que u =
et donc f(u) = f(v)f(
) = v
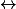
= v : contradiction .
salut
Avec les notations ci-dessus, on peut remarquer que:
f(A)=A
f(]0;1]\A)=]0;1]\A
la restriction de f à A est bijective
la restriction de f à ]0;1]\A est ]0;1]\A
Si on pose f(0)=0, f est continue en 0.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
