Exo sur les ensembles/application niveau L1

[helpmeplease1993]

Bonjour,
Je cherche quelqu'un pour m'aider a la question 10 de mon exo de mathématiques (niveau L1) (sur le liens suivant)

http://www.math.u-psud.fr/~santambr/math2-t-2011.pdf

Je n'arrive pas a démontré la question 10 donc si quelqu'un pourrait maider..
Cordialement

[Nightmare]

Hello,

qu'as-tu essayé pour le moment?

[helpmeplease1993]

Hello,

qu'as-tu essayé pour le moment?

j'ai fais:
("il existe" x apartenant a A1) ( "il existe" x appartenant a A2) => y=f(x)
"il existe" x appartenant a A1 inter A2 tel que y=f(x)
d'ou y "appartient" f(A1 inter A2)

mais aprés je sais pas. et je crois que ce que j'ai déja "fais" c'est n'importe quoi ^^

[alm]

Salut

j'ai fais:
("il existe" x apartenant a A1) ( "il existe" x appartenant a A2) => y=f(x)
"il existe" x appartenant a A1 inter A2 tel que y=f(x)
d'ou y "appartient" f(A1 inter A2)

mais aprés je sais pas. et je crois que ce que j'ai déja "fais" c'est n'importe quoi ^^

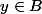
Pour donné, Il faut distinguer deux choses :
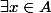
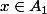
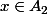
1ère : , ce qui veut dire : tel que et et .
2emme : veut dire : et
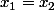
de là on déduit que mais alors rien ne dit que (ce sera vrai si est injective )
On sent donc que l'assertion est fausse et que pour construire une contre-exemple, on est guidé par cette idée: une application non injective et deux éléments distincts et de même image tel que l'un dans et l'autre dans
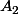
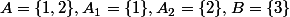
Le plus simple est de prendre par exemple et
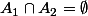
On voit que donc alors que . Je te laissele soin de meubler les ensembles pour un contre-exemple plus 'confortable' (par exemple où n'est pas vide )

[helpmeplease1993]

merci beaucoup. la je vais aller dormir mais je retravaillerais cela demain. et heureusement que j'ai poster sur le forum car j'allais dire que c'était vrai ^^