Noyau de Poisson
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Erial
- Messages: 9
- Enregistré le: 24 Nov 2015, 15:00
-
 par Erial » 24 Nov 2015, 15:33
par Erial » 24 Nov 2015, 15:33
Salut,
Pour

, on pose
=\sum_{k\in \mathbb{Z}}r^{|k|}e^{ikx})
.
Je dois montrer que
dx=1)
Je bloque car je n'arrive pas à gérer le
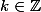
. Voilà ce que j'ai fait :
Pour
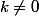
, on a :
dx=\frac{1}{2\pi}\int_{-\pi}^{\pi}\sum_{k\in \mathbb{Z}}r^{|k|}e^{ikx}dx=\frac{1}{\pi}\sum_{k \in \mathbb{Z}}\frac{r^{|k|}}{k}sin(k\pi))
J'ai interverti somme et intégrale.
Là, le souci c'est que
=0)
pour
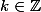
. Et je ne vois pas comment poursuivre.
Merci d'avance pour votre aide.
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 24 Nov 2015, 16:01
par arnaud32 » 24 Nov 2015, 16:01
tu appliques en effet fubini-tonelli et tu distingues dans ta siomme
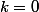
et
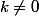
-
Erial
- Messages: 9
- Enregistré le: 24 Nov 2015, 15:00
-
 par Erial » 24 Nov 2015, 16:08
par Erial » 24 Nov 2015, 16:08
En poursuivant mes calculs, je trouve :
=-1+\sum_{k=1}^n\frac{r^{k}}{k}sin(k\pi)+\sum_{k=1}^n\frac{r^{k}}{k}sin(k\pi))
car
=sin(k\pi))
et j'ai sorti un signe moins avant.
C'est faux :mur:
-
Erial
- Messages: 9
- Enregistré le: 24 Nov 2015, 15:00
-
 par Erial » 24 Nov 2015, 16:09
par Erial » 24 Nov 2015, 16:09
P'tipito a écrit:Il faut que tu distingues avant de faire ton intégration d'ailleurs parce que
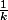
ça ne s'écrit pas quand k=0 ça peut te valoir une belle sanction (par ton prof ou même aux concours :/ )
Oui, c'est pour ça que j'ai précisé pour
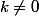
-
Erial
- Messages: 9
- Enregistré le: 24 Nov 2015, 15:00
-
 par Erial » 24 Nov 2015, 16:29
par Erial » 24 Nov 2015, 16:29
Au secours, je ne m'en sors pas avec cette somme !
-
Erial
- Messages: 9
- Enregistré le: 24 Nov 2015, 15:00
-
 par Erial » 24 Nov 2015, 17:02
par Erial » 24 Nov 2015, 17:02
Merci beaucoup !
-
Erial
- Messages: 9
- Enregistré le: 24 Nov 2015, 15:00
-
 par Erial » 24 Nov 2015, 17:16
par Erial » 24 Nov 2015, 17:16
Pour l'interversion somme/intégrale, il faut justifier que les

sont continues sur
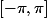
et que la série

converge uniformément sur
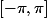
.
Bon, j'ai ensuite démontré que
=\frac{1-r^2}{1-2rcos(x)+r^2})
, pour

.
On me demande de démontrer ensuite que
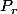
est

sur

.
Il faut donc avant tout vérifier que
+r^2 \neq 0)
pour tout
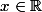
.
Est-ce correct ?
Désolé si mes questions semblent un peu naïves ^^, mais je reprends les maths petit à petit.
Merci

-
Erial
- Messages: 9
- Enregistré le: 24 Nov 2015, 15:00
-
 par Erial » 24 Nov 2015, 17:59
par Erial » 24 Nov 2015, 17:59
Ok, merci

Pour la preuve, j'ai pensé à minorer l'expression, ou alors à calculer le discriminant du trinôme de degré

en

.
Mais considérer un polynôme du second degré en

, ce n'est pas forcément une bonne idée, puisque que l'on doit montrer que le trinôme ne s'annule pas pour
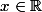
Aurais-tu une piste ?
-
Erial
- Messages: 9
- Enregistré le: 24 Nov 2015, 15:00
-
 par Erial » 24 Nov 2015, 19:10
par Erial » 24 Nov 2015, 19:10
P'tipito a écrit:calcule le déterminant, tu vas trouver qch de simple ou tu peux minorer -2rcos(x) (par rapport à x), ça marche aussi
Pas de problème pour la minoration, et j'ai le résultat voulu. :zen:
Pour l'autre méthode, je trouve
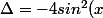\le 0)
. Mais ici, on peut avoir
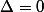
et donc une racine double pour notre polynôme ...
-
Erial
- Messages: 9
- Enregistré le: 24 Nov 2015, 15:00
-
 par Erial » 24 Nov 2015, 21:15
par Erial » 24 Nov 2015, 21:15
C'est bon :)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités