DM sur les Suites.

[badmaths]

Bonjour je suis bloqué la question suivante : démontrez que la suite (Vn) est géométrique dont on déterminera la raison et le premier terme.

Données : Vn = Un - 4
U(n+1) = 1/4*Un + 3


Ensuite la prochaine question c'est de savoir si la suite Sn = U0 + U1 + U2 +...+ Un converge ? et (Sn)/n (n>1)

merci pour votre aide

[c pi]

Au risque d'enfoncer des portes ouvertes,
je dirais que la première idée qui vient à l'esprit serait de calculer
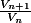à partir de ces données dont l'écriture reste ambigüe pour moi :

Vn = Un - 4
U(n+1) = 1/4*Un + 3

Si le résultat se révélait constant, ce serait une bonne "raison" pour justifier la nature géométrique de la suite considérée.

[Quidam]

Au risque d'enfoncer des portes ouvertes,

Tu as raison ; la porte était déjà ouverte ! Mais parfois il faut enfoncer la porte ouverte ! :we:

[Imod]

Sinon un calcul direct de mène aussi au résultat et la deuxième question est une conséquence directe de la première .

Imod

[badmaths]

ok merci g encor une question : quand on calcule la difference entre U(n+1)-U(n) je trouve (-3/4)U(n) + 3 . La suite est-elle croissante ou décroissante ?? ce que je ne comprends pas, c'est que je trouve un coefficient directeur négatif alors que d'après le graphique représentant la suite U(n), cette suite est croissante. Donc je bloque pour cette question qui me demande le signe de U(n+1)-U(n).

merci pr votre aide et dites moi si vous comprenez pas ma question lol merci

[Quidam]

U(n+1)-U(n) je trouve (-3/4)U(n) + 3 . La suite est-elle croissante ou décroissante ?? ce que je ne comprends pas, c'est que je trouve un coefficient directeur négatif alors que d'après le graphique représentant la suite U(n), cette suite est croissante. Donc je bloque pour cette question qui me demande le signe de U(n+1)-U(n).

Même si U(n+1)-U(n) =(-3/4)U(n) + 3, cela ne veut pas dire que la suite est décroissante (ni croissante d'ailleurs).

Si U(0)=8, alors, U(1)=5 ; sur les deux premiers termes, ça a l'air de décroître !
Si U(0)=1/2, alors U(1)=1/8+3=25/8=3.125 ; sur les deux premiers termes, ça a l'air de croître !

Dans les deux cas, ta formule est juste : U(n+1)-U(n)=(-3/4)U(n)+3. En effet :

1-er cas
U(0)=8, U(1)=5 et U(1)-U(0)=5-8=-3 qui est bien égal à (-3/4)*8+3
2-ème cas
U(0)=1/2, U(1)=25/8 et U(1)-U(0)=25/8-1/2=21/8 qui est bien égal à (-3/4)*(1/2)+3
L'un et l'autre sont possibles dans l'état actuel de mes connaissances : tu ne nous as pas donné U(0) ! Et tout va dépendre de U(0) ; donc si tu veux que l'on ait un avis sur la question, il faut nous donner davantage d'information sur ton problème !

[badmaths]

ah oui scuse moi lol U0=1 tt simplment

[badmaths]

mai y a til un moyen de dire si elle est croissante ou non sans calculer les valeurs de la suite ?

[Imod]

Et si vous utilisiez tout bêtement la suite ? Il ne faut pas oublier que les gens qui font les exercices sont rarement des imbéciles et que la suite v n'a sûrement pas été introduite par hasard .

Imod

[Quidam]

mai y a til un moyen de dire si elle est croissante ou non sans calculer les valeurs de la suite ?

Mais oui ! Mais il fallait connaître U(0) ! je me suis contenté de te montrer par deux exemples que la suite pouvait être croissante et pouvait aussi être décroissante, puisque je t'ai donné ci-dessus un exemple où la suite est décroissante et un autre où elle est croissante !

Je répète que cela dépend de U(0) !

Ici, U(0) = 1, ta suite sera croissante, mais cela résulte d'un calcul que tu n'as pas encore fait, calcul faisable en utilisant le fait que Vn est géométrique, comme l'a fait très justement remarquer Imod !

[badmaths]

merci pr cette information mais je n'y arrive malheureusement tjs pas... je ne vois pas comment utiliser le fait que V(n) soit géométrique...

[Imod]

u0+u1+...+un = 4(n+1)+v0+v1+...+vn . et la somme ne peut pas être majorée .

Imod

[Quidam]

Donc V est une suite géométrique. Comme toutes les suites géométriques bien élevées, elle peut donc s'écrire : , r étant la raison
Ensuite, puisque , ; pas si dur !
Donc
Et comme , tu peux finalement écrire :


La croissance dépend donc de !
Si , tu verras que la suite est décroissante. Et si , la suite est constante :

Par ailleurs, puisque , on a :




Le terme , somme partielle d'une suite géométrique dont la raison a une valeur absolue plus petite que 1, converge. Par contre le terme tend vers l'infini ! La suite diverge.

Que penses-tu maintenant de ?