DM pour jeudi

[LEA83600]

Bonjour j'ai un dm a faire pour Jeudi et je suis coincée a un exercice je bloque a la dernière question pouvez vous m'aider svp

[img][img]http://i21.servimg.com/u/f21/11/23/12/73/20150912.jpg[/img][/IMG]

[Carpate]

Bonjour j'ai un dm a faire pour Jeudi et je suis coincée a un exercice je bloque a la dernière question pouvez vous m'aider svp

[img][img]http://i21.servimg.com/u/f21/11/23/12/73/20150912.jpg[/img][/IMG]

Que trouves-tu pour l'aire du motif ?

[LEA83600]

Que trouves-tu pour l'aire du motif ?

33 cm² (9+24)

[Carpate]

33 cm² (9+24)

Intuitivement l'aire sera minimale quand M est au milieu de AB
Pour le démontrer reprends tes calcul en remplaçant la valeur 4 de AM par x

[capitaine nuggets]

Salut !

Avant toute chose, ce qu'il faut bien comprendre, c'est que M est un point quelconque de [AB]. BMEF est un carré où F appartient au segment [BC] donc si on fait bouger M sur [AB], F bougera sur [BC] (par exemple, si on place M en B, F sera aussi en B, donc les points B, F, M seront confondus). Ensuite, il te défini le triangle DHEG où H est sur [AD] et G sur [CD]. Le fait que DHEG soit un donné comme étant un rectangle et soit "relié" au carré BMEF par le point E t'informes sur plusieurs points :
1/ (HF) est parallèle à (AB) ;
2/ (MG) est parallèle à (AD).
En conséquence, si on fait bouger M sur [AB], alors les points F,G et H bougent respectivement sur [BC], [CD] et [AD].

Donc si on reviens au problème, on peut poser AM=x, avec x appartenant à [0,7].
1) Sachant que AB=7 et que M est un point de [AB], exprimer BM en fonction de x.
2) Déduis-en alors HD et DG en fonction de x.
3) Tu en conclus que l'aire vaut BM^2 + HD.DG :we:
4) Pour obtenir la valeur la plus petite possible, il faut trouver le minimum sur [0,7] de la fonction f définie par f(x) = BM^2 + HD.DG :++:

[LEA83600]

merci mais y a pas une explication plus simple car je n'ai pas bien compris

[Carpate]

merci mais y a pas une explication plus simple car je n'ai pas bien compris

Et tu voudrais aussi la solution prête à recopier ?

[capitaine nuggets]

je vois pas trop comment faire plus simple :

est un point qui est situé à une distance inconnue de , donc on pose 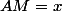, avec dans .
1/a/ Les points , , étant alignés et , que vaut 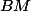en fonction de ?
b/ Déduis-en l'aire du carré .
2/a/ Que valent et en fonction de ?
b/ Déduis-en alors l'aire du rectangle .
3/ Déduis-en l'aire du motif.
4/ Pour trouver à partir de quelle(s) positions du point sur 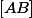, l'aire du motif est minimale, il suffit d'étudier sur l'intervalle , les variations de la fonction définie par :

[CENTER].[/CENTER]

:we:

[LEA83600]

Mon DM et terminé merci à tous pour vos réponses et à Capitaine Nuggets d'avoir pris le temps de me réexpliquer :++: :++:

[capitaine nuggets]

De rien, c'est toujours un plaisir !