Polynôme de meilleure approximation

[Sharpen]

Bonjour à tous,
Je suis actuellement en train de finir se sujet : https://banques-ecoles.fr/cms/wp-content/data/filieres-universitaires/annales-du-second-concours-de-lens-lyon/session-2010/sujet-ecrit-2010-second-concours_mathematiques.pdf
Et je bloque aux deux dernières questions : on nous demande de déterminer avec , où est l'espace vectoriel des fonctions polynômes réels (à aucun moment ils ne font référence au degré des polynômes avec le n ...) et la norme est la norme infinie sur un segment [a,b] des réels, f étant continue.
Je sais que s'annule en au moins deux points, avez-vous une piste pour déterminer , je ne vois pas très bien comment partir.
Merci .

[Ben314]

Salut,
Il y a très clairement une étourderie dans l'énoncé vu que de noter P_indice_n un truc qui dépend pas de n, le moins qu'on puisse dire, c'est que c'est étonnant (sans parler du fait que le n en question intervient dans les questions suivantes)
Bilan : Pn c'est forcément l'ensemble des polynômes de degré <=n.

C'est les questions 5 et 6 de l'exercice 2) sur lesquelles tu bloque ?
(ç'est louche que tu ait réussi à faire les 1..4 sans avoir la bonne définition pour Pn.)

[Sharpen]

Salut,
En effet, dans les questions suivantes, le intervient lorsqu'il faut montrer qu'une certaine fonction prend son maximum en au moins n+2 points. Le degré du polynôme n'est pas tellement utile. Mais du coup, si c'est bien le degré qui est question, alors ça me simplifie beaucoup la chose pour les questions suivantes. Merci.

[Ben314]

Ben, de toute façon, si tu prend l'énoncé "au pied de la lettre" avec Pn=ensemble_de_tout_les_polynômes (de degré quelconque), alors le résultat demandé à la question 1 est trivialement faux donc c'est même pas la peine de regarder la suite puisque tout parle d'un certain polynôme (qn) qui... n'existe pas en général (sauf si f est elle même un polynôme ce qui n'a aucun intérêt vu que dans ce cas, qn=f)

[Sharpen]

Je viens de regarder ce que j'ai fais, et en fait j'utilise bien un polynôme de degré n, je n'ai même pas fais attention à ça. Oui donc là, évidemment, c'est bien le degré.

[mathelot]

est ce qu'il y a une démo générale de topologie ? étant un convexe fermé.
la réponse est oui, quand la norme dérive d'un produit scalaire

[Ben314]

est ce qu'il y a une démo générale de topologie ? étant un convexe fermé

Je me rapelle plus du tout le contexte (et j'ai la flemme de reregarder), mais vu qu'il est question de polynômes et, comme par hasard, d'avoir une borne sur le degré du truc recherché, c'est qu'on doit être en dimension infinie et, dans ce cas, être "convexe fermé" est très insuffisant pour avoir forcément des projection.
Il est par exemple assez clair qu'on ne projette pas une fonction continue sur le s.e.v. formé de tout les polynômes (because pas complet, en général y'a pas de projection)

[Sharpen]

J'avais pensé à utiliser le théorème de projection sur les convexes compacts, mais je me suis rappelé que n'était pas bornée. Donc si cela reste vrai pour un convexe fermé si la norme dérive d'un produit scalaire, on peut trouver un produit scalaire (pas difficile sur les polynômes) qui caractérise cette norme ? Si c'est vrai, ça peut m'être utile pour plus tard.

[Sharpen]

J'en ai discuté avec mon professeur, et il m'a proposé l'idée de définir la norme sur une boule fermée. Voici comment j'ai rédigé :

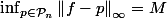
Posons . Soit la boule fermée de centre et de rayon .
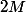
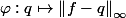
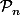
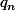
Soit l'application que l'on défini sur . On remarque que est une partie fermée (par définition) et qu'elle est bornée. Or, on a et, est un espace vectoriel de dimension finie (n+1). Par conséquent, est une partie compacte car elle est fermée et bornée en dimension finie. Et donc d'après le théorème des bornes atteintes, la fonction atteint son minimum en au moins un point d'où l'existence d'un tel que .

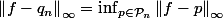
J'aurai aimé savoir si cette justification est bonne dans le cadre d'une réponse à un sujet de concours ou s'il faudrait plus de détails à certains endroits. Merci .