Valeur absolue...

par **baldurs78** » 22 Sep 2006, 13:47

ReBonjour,

Une piste me suffirait , ou un exemple , bref voila mon equation avec laquelle je suis pas très ami...

|x|

<

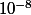
Merci pour vos futurs réponses

par **Imod** » 22 Sep 2006, 14:04

Il me semble qu'il suffit de majorer

et

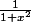
et tu as immédiatement un majorant de

.

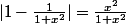
Imod

par **Flodelarab** » 22 Sep 2006, 14:39

baldurs78 a écrit:ReBonjour,

Une piste me suffirait , ou un exemple , bref voila mon equation avec laquelle je suis pas très ami...

|x| <

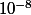
Merci pour vos futurs réponses

Ne voyant qu'un x, on peut aussi partir de

et aller de proche en proche vers x:

....

par **nada-top** » 22 Sep 2006, 15:02

Flodelarab a écrit:Ne voyant qu'un x, on peut aussi partir de

et aller de proche en proche vers x:

....

plutot partir de

pour en arriver à

non?..ce qui revient à démontrer l'implication réciproque :

par **Flodelarab** » 22 Sep 2006, 15:18

nada-top a écrit:plutot partir de pour en arriver à non?..ce qui revient à démontrer l'implication réciproque :

OUI
aussi

:++:

par **pitchoune** » 22 Sep 2006, 15:28

Pour moi, m'énoncé étant |x| [/B] |(1/(1+x²)) -1| < 10^-8, il faut partir du |x|<10^-4 et ajouter au fur et à mesure les élément.

Au final, j'arrive |(1/(1+x²))-1| < (10^-8/(1+10^-8))

et (10^-8/(1+10^-8)) < 10^-8

par **nada-top** » 22 Sep 2006, 15:43

Pour moi, m'énoncé étant |x| |(1/(1+x²)) -1| < 10^-8, il faut partir du |x|<10^-4 et ajouter au fur et à mesure les élément.

démontrer

ou

ça revient au meme : démontrer

équivaut à démontrer

par **Imod** » 22 Sep 2006, 17:20

Pour moi la méthode la plus directe et la plus simple :

Si

alors

et

.
Et en multipliant membre à membre on obtient :

.

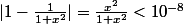
Imod

par **baldurs78** » 22 Sep 2006, 20:04

Merci pour vos réponse,

Je les ai lu et j'ai essayer d'abord de partir de l'encadrement de |(1/(1+x^2))-1) , mais je suis pas arriver a revenir a x<10^-4

LA réponse la plus simple est a mon avis celle de Imod sauf que je comprend pas comment tu passes a cela :

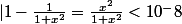
je n'y arrives pas dsl...

par **Imod** » 22 Sep 2006, 20:14

Pour l'égalité tu mets au même dénominateur et pour l'inégalité il suffit de remarquer que :

.

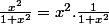
Imod

par **baldurs78** » 22 Sep 2006, 20:20

Ou il fait tard ou je comprend vraimen pas ^^

OK

OK

On multiplie:

d'ou

mais après comment tu arrive au résultat

Par quelle propriété on peut passer aux valeur absolu...?

par **tize** » 22 Sep 2006, 22:47

J'ai pas tout suivi mais il me semble quand même que :

par **Imod** » 22 Sep 2006, 23:01

Il me semblait pourtant avoir tout dit "pour l'égalité il suffit de réduire au même dénominateur" . S'il faut détailler allons-y :

.

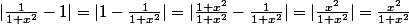
Imod

P.S : Tout ce que j'ai dit depuis le début était contenu dans mon premier message .

Valeur absolue...

Valeur absolue...

oui...

heu...

Qui est en ligne