"Défi" Intégrales T*S
22 messages
- Page 1 sur 2 - 1, 2
"Défi" Intégrales T*S
Bonjour à tous.J'ai un exercice à faire en DM pour la rentrée. J'ai réussi le finir, mais je trouve que ma façon de calculer la primitive n'est pas très rigoureuse. J'aimerais avoir vos avis.
Voici l'énoncé :
Défi : f est la fonction affine définie sur R par f(x)=-3X+2 et g la fonction définie par g(x)= f(f(f(...f(X)...))) où f apparaît 2015 fois.
Calculer l'intégrale de 0 à 1 de G(X)
Voici mes résultats :
f(X)=-3X+2
J'ai d'abord calculé f[f(X)]=9X-4
Puis f(f[f(X)])=-27X+14
J'ai trouvé comme formule 3^n X -[(3^n -1)/2] (pour f apparaissant n fois) pour la généraliser il faut utiliser la récurrence sauf que je ne voit pas comment mettre en place une récurrence.
Pour la suite, une fois la récurrence établie, donc que la formule est validée pour n=2015, il reste à calculer la primitive puis l'intégrale, ce qui nous donne 1/2.
Voila donc si vous pouvez m'aider pour la récurrence :) Merci d'avance, bonne journée ! =)
Voici l'énoncé :
Défi : f est la fonction affine définie sur R par f(x)=-3X+2 et g la fonction définie par g(x)= f(f(f(...f(X)...))) où f apparaît 2015 fois.
Calculer l'intégrale de 0 à 1 de G(X)
Voici mes résultats :
f(X)=-3X+2
J'ai d'abord calculé f[f(X)]=9X-4
Puis f(f[f(X)])=-27X+14
J'ai trouvé comme formule 3^n X -[(3^n -1)/2] (pour f apparaissant n fois) pour la généraliser il faut utiliser la récurrence sauf que je ne voit pas comment mettre en place une récurrence.
Pour la suite, une fois la récurrence établie, donc que la formule est validée pour n=2015, il reste à calculer la primitive puis l'intégrale, ce qui nous donne 1/2.
Voila donc si vous pouvez m'aider pour la récurrence :) Merci d'avance, bonne journée ! =)
bonjour
il semble que la formule generale que tu as trouvé soit fausse
1- elle ne donne pas une alternance de signe avec n il manque un (-1)^n en facteur sans doute
2- le terme constant pour n = 3 donne 13 et non 14
de meme il faut sans doute introduire un coefficient pour obtenir quelque chose du genre 3^n -(-1)^n qui conduit a ajouter ou retrancher 1 selon la valeur de n
ensuite il faut montrer que f(n+1) est bien egale. 3f(n) + 2
f( n+1) = (3^(n+1) *x -[...] = 3(3^n) x - 3[...] ....
il semble que la formule generale que tu as trouvé soit fausse
1- elle ne donne pas une alternance de signe avec n il manque un (-1)^n en facteur sans doute
2- le terme constant pour n = 3 donne 13 et non 14
de meme il faut sans doute introduire un coefficient pour obtenir quelque chose du genre 3^n -(-1)^n qui conduit a ajouter ou retrancher 1 selon la valeur de n
ensuite il faut montrer que f(n+1) est bien egale. 3f(n) + 2
f( n+1) = (3^(n+1) *x -[...] = 3(3^n) x - 3[...] ....
Il y a une suite arithmetico-géométrique là dedans, sais-tu les résoudre ? Ca peut aider.
Fixons x_0 un réel quelconque.
En définissant_{n \in \mathbb{N}}) par :
par :
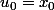 et
et
 = -3 u_n + 2)
Ainsi, = u_{2015})
Ta suite est définie par son premier terme x_0 et une relation de récurrence définie par une fonction affine : c'est une suite arithmético-géométrique.
On sait la résoudre avec une suite auxiliaire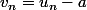 qui est géométrique si a est bien choisi.
qui est géométrique si a est bien choisi.
Quand tu auras u_n en fonction de n et x_0, tu pourras calculer g(x0) = u_2015
EDIT : j'ai trouvé a = 1/2 et^n (x0 - 1/2) + 1/2) . A vérifier...
. A vérifier...
Fixons x_0 un réel quelconque.
En définissant
Ainsi,
Ta suite est définie par son premier terme x_0 et une relation de récurrence définie par une fonction affine : c'est une suite arithmético-géométrique.
On sait la résoudre avec une suite auxiliaire
Quand tu auras u_n en fonction de n et x_0, tu pourras calculer g(x0) = u_2015
EDIT : j'ai trouvé a = 1/2 et
RE
Bien sur je suis d'accord, mais ......
je parlais de la formule generale donne par dogblue qui a ((3^n)-1)/2 pour le terme constant soit (27-1)/2=13 pour n = 3
d'ou .......
annick a écrit:@ siger : excuse-moi, mais je suis bien d'accord avec dogblue pour le 14 de n=3 (et non 13 comme tu le dis)
f1=-3x+2
f2=-3f0+2=-3(-3x+2)+2=9x-6+2=9x-4
f3=-3f1+2=-3(9x-4)+2=-27x+12+2=-27x+14
Bien sur je suis d'accord, mais ......
je parlais de la formule generale donne par dogblue qui a ((3^n)-1)/2 pour le terme constant soit (27-1)/2=13 pour n = 3
d'ou .......
f' constante
soit g.
Comme f est affine, la dérivation de f donne un facteur -3
d'où=(-3)^n)
d'où= (-3)^n x +K) (K: constante d'intégration)
(K: constante d'intégration)
Comme il existe un point fixe tel que f(c)=c,
c est point fixe de g.

on calcule à l'aide du point fixe c:
à l'aide du point fixe c:
^n c +K)
=(-3)^n x +c (1-(-3)^{n}))
=(-3)^n x +\frac{1}{2} (1-(-3)^{n}))
Comme f est affine, la dérivation de f donne un facteur -3
d'où
d'où
Comme il existe un point fixe tel que f(c)=c,
c est point fixe de g.
on calcule
chombier a écrit:On s'aperçoit d'ailleurs, en intégrant, que quelle que soit la valeur de n, l'intégrale de g entre 0 et 1 vaudra 1/2. Etonnant !
salut
le changement de coordonnées : (translation qui conserve les aires)
X = x - 1/2
Y = y - 1/2
conduit à y = f(x) Y = -3X = h(X)
alors calculer g = f o f o ... o f n fois revient à calculer G = h o h o ... o h n fois
et intégrer g sur [0, 1] revient à intégrer G sur [-1/2, -1/2]
or h est impair donc G aussi donc l'intégrale est nulle pour tout n et donc elle est constante quelle que soit n
il en donc de même pour g et il suffit de calculer
:zen:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
mathelot a écrit:soit g.
Comme f est affine, la dérivation de f donne un facteur -3
d'où
d'où(K: constante d'intégration)
Comme il existe un point fixe tel que f(c)=c,
c est point fixe de g.
on calculeà l'aide du point fixe c:
C'est très joli. J'ai juste eu du mal à voir pourquoi g'(x) = (-3)^n :
Comme
Très joli ! Le coup du point fixe est très bien trouvé, lui aussi !
chan79 dit exactement en terme intégrale ce que je dis en terme géométrique ...
PS :: c'est exactement ce que je cherchais à faire en plus .... et j'ai merdé sur ma formule (de récurrence) .... c'est pourquoi j'ai effectué la translation ...
PS :: c'est exactement ce que je cherchais à faire en plus .... et j'ai merdé sur ma formule (de récurrence) .... c'est pourquoi j'ai effectué la translation ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Tout d'abord merci à vous d'avoir répondu. :++:
Je n'ai pas étudié tout ce qui se rapporte au point fixe, et les notations telles que "f o f o f", donc je vais éviter d'utiliser cela.
Je pensais essayer avec la technique donnée par chan79 car cela me parait simple et efficace (non pas que les autres n'aillent pas, bien au contraire :happy2: )
Juste petite remarque, cela me parait plus clair de calculer I1, puis après de mettre la forme générale de dire que c'est constant (en inversant l'ordre de lequel chan79 l'a présenté), on est d'accord que ça ne pose pas de problème ?! :lol3:
Je vais recopier tout ça au propre, normalement je n'aurais plus de questions !
Je tiens par ailleurs à vous remercier tout particulièrement pour votre aide, car -sans faire de mauvaise pub-, j'ai été sur quelques autres forum et les réponses étaient bien plus confuses. Je n'attendais même pas tant de précisions de votre part, mais merci beaucoup, et bonne soirée à vous :++:
Je n'ai pas étudié tout ce qui se rapporte au point fixe, et les notations telles que "f o f o f", donc je vais éviter d'utiliser cela.
Je pensais essayer avec la technique donnée par chan79 car cela me parait simple et efficace (non pas que les autres n'aillent pas, bien au contraire :happy2: )
Juste petite remarque, cela me parait plus clair de calculer I1, puis après de mettre la forme générale de dire que c'est constant (en inversant l'ordre de lequel chan79 l'a présenté), on est d'accord que ça ne pose pas de problème ?! :lol3:
Je vais recopier tout ça au propre, normalement je n'aurais plus de questions !
Je tiens par ailleurs à vous remercier tout particulièrement pour votre aide, car -sans faire de mauvaise pub-, j'ai été sur quelques autres forum et les réponses étaient bien plus confuses. Je n'attendais même pas tant de précisions de votre part, mais merci beaucoup, et bonne soirée à vous :++:
22 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
